【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
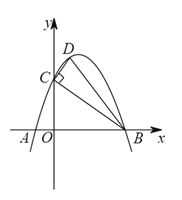
(1)求此抛物线的解析式.
(2)以点![]() 为直角顶点作直角三角形
为直角顶点作直角三角形![]() ,斜边
,斜边![]() 与抛物线交于点
与抛物线交于点![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)将![]() 绕着它的顶点
绕着它的顶点![]() 顺时针在第一象限内旋转,旋转的角度为
顺时针在第一象限内旋转,旋转的角度为![]() ,旋转后的图形为
,旋转后的图形为![]() .当
.当
旋转后的![]() 有一边与
有一边与![]() 重合时,求
重合时,求![]() 不在
不在![]() 上的顶点的坐标.
上的顶点的坐标.
参考答案:
【答案】(![]() )
)![]() (
(![]() )
)![]() ;(
;(![]() )见解析.
)见解析.
【解析】分析:(1)根据抛物线与x轴交于A(-2-n,0),B(4+n,0)两点,根据根与系数的关系求出m的值,从而求出解析式.(2)先求出A、B、C、D的坐标,设出点P 的坐标,由CP=EP即可求解;(3)分两种情况讨论:①![]() 与
与![]() 重合;
重合;![]() 与
与![]() 重合.
重合.
本题解析:
(![]() )
)![]() ,
,
即![]() ,
,
![]() ,
,
![]() .
.
(![]() )
)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
(![]() )①
)①![]() 与
与![]() 重合,
重合,
过![]() 作
作![]() ,
,
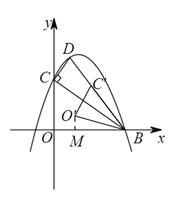
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
即![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
②![]() 与
与![]() 重合时,过
重合时,过![]() 作
作![]() 轴,
轴,
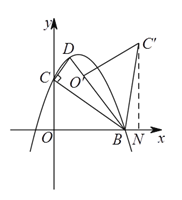
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
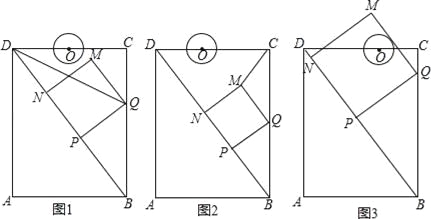
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<
 ).
).(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算结果正确的是( )
A.a+a=a2
B.(a﹣1)2=a2﹣1
C.aa=a2
D.(3a)3=9a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2﹣2mx+m2+m﹣1(m是常数)的顶点为P,直线
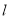 :y=x﹣1
:y=x﹣1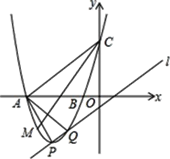
(1)求证:点P在直线
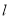 上;
上;(2)当m=﹣3时,抛物线与x轴交于A,B两点,与y轴交于点C,与直线
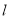 的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;(3)若以抛物线和直线
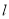 的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.
的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0
B.m>0,n<0
C.m<0,n>0
D.m<0,n<0 -
科目: 来源: 题型:
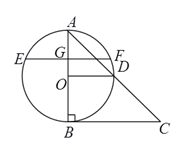
查看答案和解析>>【题目】如图,在
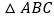 中,
中,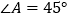 .以
.以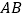 为直径的⊙
为直径的⊙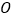 与
与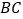 相切于
相切于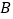 ,交
,交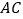 于点
于点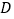 ,
,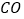 的延长线交⊙
的延长线交⊙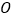 于点
于点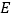 ,过点作弦
,过点作弦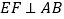 ,垂足为点
,垂足为点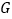 .
.
(1)求证:①
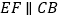 ,②
,② .
.(2)若
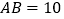 ,求
,求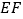 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算 (-a)2·a3结果是 ( )
A. a6 B. a5 C. -a6 D. -a5
相关试题

