【题目】如图,在![]() 中,
中,![]() .以
.以![]() 为直径的⊙
为直径的⊙![]() 与
与![]() 相切于
相切于![]() ,交
,交![]() 于点
于点![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() ,过点作弦
,过点作弦![]() ,垂足为点
,垂足为点![]() .
.
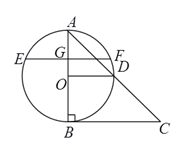
(1)求证:①![]() ,②
,②![]() .
.
(2)若![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(![]() )①证明见解析;②证明见解析;(
)①证明见解析;②证明见解析;(![]() )4
)4![]() .
.
【解析】(1) ①由切线的性质和垂径定理即可得证;(2)连接BD,由直径所对的圆周角为90°和等腰三角形的性质以及已知条件证明结论即可;(2)AB=2,则圆的直径为2,所以半径为1,即OB=OE=1,利用勾股定理求出CO的长,再通过证明△EOG∽△COB得到关于EG的比例式可求出EG的长,进而求出EF的长.
本题解析:
(![]() )①∵
)①∵![]() 为切线,切点为
为切线,切点为![]() ,
,![]() 为直径,∴
为直径,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
②连接![]() .
.
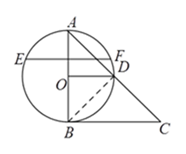
∵![]() 为直径,点
为直径,点![]() 在⊙
在⊙![]() 上,∴
上,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
(![]() )∵
)∵![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() ,
,![]() ,
,
∴(![]() )①∵
)①∵![]() 为切线,切点为
为切线,切点为![]() ,
,![]() 为直径,∴
为直径,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
②连接![]() .
.

∵![]() 为直径,点
为直径,点![]() 在⊙
在⊙![]() 上,∴
上,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
(![]() )∵
)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2﹣2mx+m2+m﹣1(m是常数)的顶点为P,直线
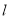 :y=x﹣1
:y=x﹣1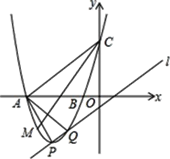
(1)求证:点P在直线
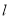 上;
上;(2)当m=﹣3时,抛物线与x轴交于A,B两点,与y轴交于点C,与直线
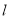 的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;(3)若以抛物线和直线
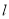 的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.
的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值. -
科目: 来源: 题型:
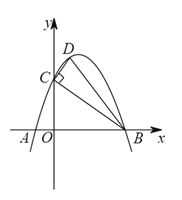
查看答案和解析>>【题目】如图,抛物线
 与
与 轴交于
轴交于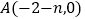 ,
, 两点(
两点(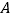 在
在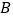 的左侧),与
的左侧),与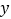 轴交于点
轴交于点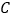 ,顶点为
,顶点为 .
.
(1)求此抛物线的解析式.
(2)以点
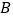 为直角顶点作直角三角形
为直角顶点作直角三角形 ,斜边
,斜边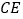 与抛物线交于点
与抛物线交于点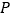 ,且
,且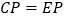 ,求点
,求点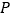 的坐标.
的坐标.(3)将
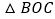 绕着它的顶点
绕着它的顶点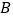 顺时针在第一象限内旋转,旋转的角度为
顺时针在第一象限内旋转,旋转的角度为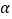 ,旋转后的图形为
,旋转后的图形为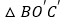 .当
.当旋转后的
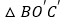 有一边与
有一边与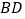 重合时,求
重合时,求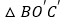 不在
不在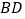 上的顶点的坐标.
上的顶点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0
B.m>0,n<0
C.m<0,n>0
D.m<0,n<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算 (-a)2·a3结果是 ( )
A. a6 B. a5 C. -a6 D. -a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
(2)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】羊年除夕当日微信红包收发总量达80.8亿个.其中80.8亿用科学记数法可表示为( )
A.8.08×108
B.0.808×109
C.8.08×109
D.0.808×1010
相关试题

