【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.
(1)直接写出∠NDE的度数;
(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;
(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=![]() ,其他条件不变,求线段AM的长.
,其他条件不变,求线段AM的长.

参考答案:
【答案】(1)∠NDE=90°;(2)不变;(3)![]() .
.
【解析】
试题分析:(1)证明△MAC≌△NBC即可;
(2)与(1)的证明方法相似,证明△MAC≌△NBC即可;
(3)作GK⊥BC于K,证明AM=AG,根据△MAC≌△NBC,得到∠BDA=90°,根据直角三角形的性质和已知条件求出AG的长,得到答案.
试题解析:(1)∵∠ACB=90°,∠MCN=90°,∴∠ACM=∠BCN,在△MAC和△NBC中,∵AC=BC,∠ACM=∠BCN,MC=NC,∴△MAC≌△NBC,∴∠NBC=∠MAC=90°,又∵∠ACB=90°,∠EAC=90°,∴∠NDE=90°;
(2)不变,在△MAC≌△NBC中,∵AC=BC,∠ACM=∠BCN,MC=NC,∴△MAC≌△NBC,∴∠N=∠AMC,又∵∠MFD=∠NFC,∠MDF=∠FCN=90°,即∠NDE=90°;
(3)作GK⊥BC于K,∵∠EAC=15°,∴∠BAD=30°,∵∠ACM=60°,∴∠GCB=30°,∴∠AGC=∠ABC+∠GCB=75°,∠AMG=75°,∴AM=AG,∵△MAC≌△NBC,∴∠MAC=∠NBC,∴∠BDA=∠BCA=90°,∵BD=![]() ,∴AB=
,∴AB=![]() ,AC=BC=
,AC=BC=![]() ,设BK=a,则GK=a,CK=
,设BK=a,则GK=a,CK=![]() ,∴
,∴![]() ,∴a=1,∴KB=KG=1,BG=
,∴a=1,∴KB=KG=1,BG=![]() ,AG=
,AG=![]() ,∴AM=
,∴AM=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.哥哥的身高比弟弟高是必然事件
B.今年中秋节有雨是不确定事件
C.随机抛一枚均匀的硬币两次,都是正面朝上是不可能事件
D.“彩票中奖的概率为 ”表示买5张彩票肯定会中奖
”表示买5张彩票肯定会中奖 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
在一个三角形中,各边和它所对角的正弦的比相等,
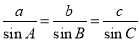 ,利用上述结论可以求解如下题目:
,利用上述结论可以求解如下题目:在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.
解:在△ABC中,∵
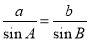 ,∴
,∴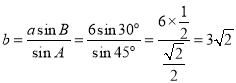 .
.理解应用:
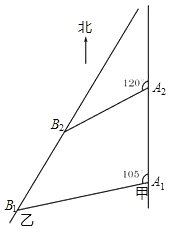
如图,甲船以每小时
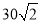 海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距
海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距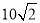 海里.
海里.(1)判断△A1A2B2的形状,并给出证明;
(2)求乙船每小时航行多少海里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O半径为6,点O到直线l的距离是5,则直线l与⊙O位置关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程ax2﹣bx﹣6=0的一个根为x=2,则2a﹣b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级实行小组合作学习,为了解学生课堂发言情况,随机抽取该年级部分学生,对他们每天在课堂中发言的次数进行调查和统计,统计表如下,并绘制了两幅不完整的统计图(如图所示).已知A、B两组发言人数直方图高度比为1∶5,请结合图中相关的数据回答下列问题:
发言次数n
A
0≤n<5
B
5≤n<10
C
10≤n<15
D
15≤n<20
E
20≤n<25
F
25≤n<30

(1)A组的人数是多少?本次调查的样本容量是多少?
(2)求出C组的人数,并补全直方图;
(3)该校七年级共有250人.请估计全年级每天在课堂中发言次数不少于15次的人数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某人的钱包内有10元钱、20元钱和50元钱的纸币各1张,从中随机取出2张纸币.
(1)求取出纸币的总额是30元的概率;
(2)求取出纸币的总额可购买一件51元的商品的概率.
相关试题

