【题目】把(sinα)2记作sin2α,根据图1和图2完成下列各题.
(1)sin2A1+cos2A1= ,sin2A2+cos2A2= ,sin2A3+cos2A3= ;
(2)观察上述等式猜想:在Rt△ABC中,∠C=90°,总有sin2A+cos2A= ;
(3)如图2,在Rt△ABC中证明(2)题中的猜想:
(4)已知在△ABC中,∠A+∠B=90°,且sinA=![]() ,求cosA.
,求cosA.

参考答案:
【答案】(1)1、1、1;(2)1;(3)证明见解析;(4)![]() .
.
【解析】试题分析:(1)根据正弦函数和余弦函数的定义分别计算可得;
(2)由(1)中的结论可猜想sin2A+cos2A=1;
(3)由sinA=![]() 、cosA=
、cosA=![]() 且a2+b2=c2知sin2A+cos2A=(
且a2+b2=c2知sin2A+cos2A=(![]() )2+(
)2+(![]() )2=
)2=![]() =
=![]() =1;
=1;
(4)根据直角三角形中sin2A+cos2A=1知(![]() )2+cosA2=1,据此可得答案.
)2+cosA2=1,据此可得答案.
试题解析:解:(1)sin2A1+cos2A1=(![]() )2+(
)2+(![]() )2=
)2=![]() =1,sin2A2+cos2A2=(
=1,sin2A2+cos2A2=(![]() )2+(
)2+(![]() )2=
)2=![]() +
+![]() =1,sin2A3+cos2A3=(
=1,sin2A3+cos2A3=(![]() )2+(
)2+(![]() )2=
)2=![]() =1,故答案为:1、1、1;
=1,故答案为:1、1、1;
(2)观察上述等式猜想:在Rt△ABC中,∠C=90°,总有sin2A+cos2A=1,故答案为:1;
(3)在图2中,∵sinA=![]() ,cosA=
,cosA=![]() ,且a2+b2=c2,则sin2A+cos2A=(
,且a2+b2=c2,则sin2A+cos2A=(![]() )2+(
)2+(![]() )2=
)2=![]() =
=![]() =1,即sin2A+cos2A=1;
=1,即sin2A+cos2A=1;
(4)在△ABC中,∠A+∠B=90°,∴∠C=90°,∵sin2A+cos2A=1,∴( ![]() )2+cosA2=1,解得:cosA=
)2+cosA2=1,解得:cosA=![]() 或cosA=﹣
或cosA=﹣![]() (舍),∴cosA=
(舍),∴cosA=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
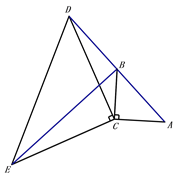
(1)求证:△ACD≌△BCE;
(2) 若AC=3cm,求BE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P的坐标为(a﹣1,5﹣2a),且它到两个坐标轴的距离相等,则点P的坐标为( )
A.(3,3)B.(3,﹣3)C.(1,﹣1)D.(1,1)或(3,﹣3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】比—3大的负整数是_____________,比3小的非负整数是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为⊙O直径,D是
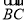 的中点,DE⊥AC交AC的延长线于E,⊙O的切线交AD的延长线于F.
的中点,DE⊥AC交AC的延长线于E,⊙O的切线交AD的延长线于F.(1)求证:直线DE与⊙O相切;
(2)已知DG⊥AB且DE=4,⊙O的半径为5,求tan∠F的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品因换季准备打折出售,如果按照原定价的七五折出售,每件将赔25元,而按原定价的九折出售,每件将赚20元,则这种商品的原定价是( )
A.200元B.300元C.320元D.360元
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示:425000=_____.
相关试题

