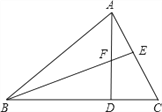
【题目】如图,AD是△ABC的高,E为AC上一点, BE交AD于F,且有DC=FD,AC=BF.
(1)说明△BFD≌△ACD;
(2)若![]() ,求AD的长;
,求AD的长;
(3)请猜想BF和AC的位置关系并说明理由.
参考答案:
【答案】(1)证明见解析;(2)AD=![]() ;(3)BF⊥AC.
;(3)BF⊥AC.
【解析】试题分析:(1)在Rt△ACD和Rt△BFD中,根据直角边DC=FD和斜边AC=BF对应相等,可证明△BFD≌△ACD;
(2)由(1)知:AD=BD,又AD⊥BC,△ADB为等腰直角三角形,已知斜边AB的长,运用勾股定理可将AD的长求出;
(3)由△ADC≌△BDF,得到∠EBC=∠DAC,又因为∠DAC+∠ACD=90°,所以∠EBC+∠ACD=90°,则BE⊥AC,即BF⊥AC.
试题解析:解:(1)∵AD是ABC的高,∴△ACD与△BFD都是直角三角形,
∵DC=FD,AC=BF,∴Rt△ACD≌Rt△BFD.
(2)∵Rt△ACD≌Rt△BFD,∴AD=BD.
在Rt△ACD中,∵AD2+BD2=AB2,∴2AD2=AB2,∴AD=![]() ;
;
(3)∵△ADC≌△BDF,∴∠EBC=∠DAC.
又∵∠DAC+∠ACD=90°,∴∠EBC+∠ACD=90°,∴∠BEC=90°,∴BE⊥AC,即BF⊥AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,∠C=90°,AC=6,BC=8,M是BC的中点,P为AB上的一个动点(不可以与A,B重合),并作∠MPD=90°,PD交BC(或BC的延长线)于点D
(1)记BP的长为x,△BPM的面积为y,求y与x的函数关系式,并写出自变量x的取值范围。
(2)是否存在这样的点P,使得△MPD与△ABC相似?若存在,请求出x的值;若不存在,请说明理由

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列因式分解中,正确的是( )
A. x2y2﹣z2=x2(y+z)(y﹣z) B. ﹣x2y+4xy=﹣xy(x+4)
C. 9﹣12a+4a2=﹣(3﹣2a)2 D. (x+2)2﹣9=(x+5)(x﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣1,0),B(1,1),把线段AB平移,使点B移动到点D(3,4)处,这时点A移动到点C处.
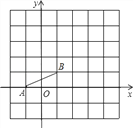
(1)写出点C的坐标__________;
(2)求经过C、D的直线与y轴的交点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和比外角和多1080°,并且这个多边形的各内角都相等,则这个多边形的每一个外角等于_______.
-
科目: 来源: 题型:
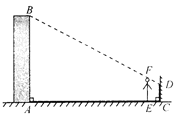
查看答案和解析>>【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本,小亮用31元买了同样的钢笔2支和笔记本5本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会表现突出的同学,要求笔记本数不少于钢笔数.请问:有多少购买方案?请你一一写出.
相关试题

