【题目】学校准备购置甲乙两种羽毛球拍若干,已知甲种球拍的单价比乙种球拍的单价多40元,且购买4副甲种球拍与购买6副乙种球拍的费用相同.
(1)两种球拍的单价各是多少元?
(2)若学校准备购买100副甲乙两种羽毛球拍,且购买甲种球拍的费用不少于乙种球拍费用的3倍,问购买多少副甲种球拍总费用最低?
参考答案:
【答案】
(1)解:设甲种球拍的单价为x元,乙种球拍的单价为(x﹣40)元,
根据题意得,4x=6(x﹣40),
解得:x=120,
x﹣40=80,
答:甲种球拍的单价为120元,乙种球拍的单价80元
(2)解:设购买m副甲种球拍总费用最低,总费用为y元,
根据题意得,120m≥3×80(100﹣m),
解得:m≥ ![]() ,
,
∵y=120m+80(100﹣m)=40m+8000
∵40>0,
∴当m取最小值时,总费用为y最小,
∴m=67时,总费用为y最小,
答:购买67副甲种球拍总费用最低
【解析】(1)设甲种球拍的单价为x元,乙种球拍的单价为(x﹣40)元,根据题意列方程即可得到结论;(2)设购买m副甲种球拍总费用最低,总费用为y元,根据题意列不等式得到m≥ ![]() ,根据函数的性质即可得到结论.
,根据函数的性质即可得到结论.
-
科目: 来源: 题型:
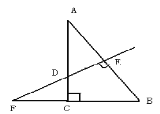
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交BC的延长线于F,若∠F=30°,DE=1,则EF的长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC是等边三角形,D、E分别是BC、AC上一点,且AE=CD,AD,AD、BE交于P,过B作BQ⊥AD于Q,若QP=3cm,PE=1cm,求AD的长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初二年级抽取部分学生进行跳绳测试,并规定:每分钟跳90次以下的为不及格;每分钟跳90~99次的为及格;每分钟100~109次的为中等;每分钟110~119次的为良好;每分钟120次及以上的为优秀。测试结果整理绘制成如下两幅不完整的统计图。请根据图中信息,解答下列各题:

(1)参加这次跳绳测试的共有人;
(2)补全条形统计图;
(3)在扇形统计图中,“中等”部分所对的圆心角的度数是;
(4)如果该校初二年级的总人数是480人,根据此统计数据,请你估算出该校初二年级跳绳成绩为“优秀”的人数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC的底边长为8cm,腰长为5cm,一动点P在底边上从B向C以0.25cm/s的速度移动,请你探究:当P运动几秒时,P点与顶点A的连线PA与腰垂直。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 (x>0)的图像交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=.
(x>0)的图像交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将
 ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将
ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将  CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).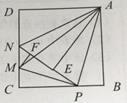
① CMP∽
CMP∽  BPA;
BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2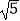 ;
;
⑤当 ABP≌
ABP≌  AND时,BP=4
AND时,BP=4 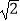 -4.
-4.
A.①②③
B.②③⑤
C.①④⑤
D.①②⑤
相关试题

