【题目】如图所示,△ABC是等边三角形,D、E分别是BC、AC上一点,且AE=CD,AD,AD、BE交于P,过B作BQ⊥AD于Q,若QP=3cm,PE=1cm,求AD的长。

参考答案:
【答案】7cm
【解析】
根据题意通过“边角边”证明△BAE≌△ACD,得到BE=AD,∠DAC=∠EBA,根据三角形外角的性质求得∠BPQ=60°,然后在Rt△BQP中,求得BP的长,则根据AD=BE=BP+PE即可得到答案.
解:∵△ABC是等边三角形,
∴∠BAC=∠C=60°,AB=AC,
又∵AE=CD,
∴△BAE≌△ACD(SAS),
∴BE=AD,∠DAC=∠EBA,
∴∠BPQ=∠EBA+∠BAP=∠DAC +∠BAP=60°,
又∵BQ⊥AD,
∴∠BQP=90°,
∴∠QBP=30°,
∴QP=![]() BP,
BP,
∵QP=3,
∴BP=6,
∵PE=1,
∴AD=BE=BP+PE=6+1=7.
答:AD的长为7cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我省某工艺厂为全运会设计了一款成本为每件20元的工艺品,投放市场试销后发现每天的销售量y(件)是售价x(元/件)的一次函数。当售价为22元/件时,每天销售量为780件;当售价为25元/件时,每天销售量为750件。
(1)求y与x的函数关系式;
(2)如果该工艺品售价最高不超过每件30元,那么售价定为每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?(利润=售价-成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,山坡上有一颗树AB,树底部B点到山脚C点的距离BC为6
 米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
-
科目: 来源: 题型:
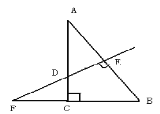
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交BC的延长线于F,若∠F=30°,DE=1,则EF的长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初二年级抽取部分学生进行跳绳测试,并规定:每分钟跳90次以下的为不及格;每分钟跳90~99次的为及格;每分钟100~109次的为中等;每分钟110~119次的为良好;每分钟120次及以上的为优秀。测试结果整理绘制成如下两幅不完整的统计图。请根据图中信息,解答下列各题:

(1)参加这次跳绳测试的共有人;
(2)补全条形统计图;
(3)在扇形统计图中,“中等”部分所对的圆心角的度数是;
(4)如果该校初二年级的总人数是480人,根据此统计数据,请你估算出该校初二年级跳绳成绩为“优秀”的人数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购置甲乙两种羽毛球拍若干,已知甲种球拍的单价比乙种球拍的单价多40元,且购买4副甲种球拍与购买6副乙种球拍的费用相同.
(1)两种球拍的单价各是多少元?
(2)若学校准备购买100副甲乙两种羽毛球拍,且购买甲种球拍的费用不少于乙种球拍费用的3倍,问购买多少副甲种球拍总费用最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC的底边长为8cm,腰长为5cm,一动点P在底边上从B向C以0.25cm/s的速度移动,请你探究:当P运动几秒时,P点与顶点A的连线PA与腰垂直。

相关试题

