【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF. 
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
参考答案:
【答案】
(1)证明:∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDE均为直角三角形,
∵ ![]()
∴△BDE≌△CDF,
∴DE=DF,即AD平分∠BAC
(2)AB+AC=2AE.
证明:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF,
在△AED与△AFD中,
∵  ,
,
∴△AED≌△AFD,
∴AE=AF,
∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE
【解析】(1)根据相“HL”定理得出△BDE≌△CDF,故可得出DE=DF,所以AD平分∠BAC;(2)由(1)中△BDE≌△CDE可知BE=CF,AD平分∠BAC,故可得出△AED≌△AFD,所以AE=AF,故AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.
【考点精析】掌握角平分线的性质定理是解答本题的根本,需要知道定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OC平分∠AOB,CD⊥OA于D,CE⊥OB于E,连接DE,猜想DE与OC的位置关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“若a>b,则|a|>|b|”是______命题.(填“真”或“假”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
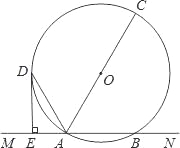
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】1不是﹣1的( )
A.相反数B.绝对值C.平方数D.倒数
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别
A型
B型
AB型
O型
频率
0.4
0.35
0.1
0.15
A. 16人 B. 14人 C. 4人 D. 6人
-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励居民节约用电,我市自2012年以来对家庭用电收费实行阶梯电价,即每月对每户居民的用电量分为三个档级收费,第一档为用电量在180千瓦时(含180千瓦时)以内的部分,执行基本价格;第二档为用电量在180千瓦时到450千瓦时(含450千瓦时)的部分,实行提高电价;第三档为用电量超出450千瓦时的部分,执行市场调节价格.我市一位同学家今年2月份用电330千瓦时,电费为213元,3月份用电240千瓦时,电费为150元.已知我市的一位居民今年4、5月份的家庭用电量分别为160和 410千瓦时,请你依据该同学家的缴费情况,计算这位居民4、5月份的电费分别为多少元?
相关试题

