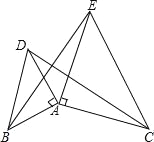
【题目】如图,已知AB=AD,AC=AE,∠BAD=∠CAE=90°,试判断CD与BE的大小关系和位置关系,并进行证明.
参考答案:
【答案】CD=BE,CD⊥BE.
【解析】
利用等腰直角三角形的性质和全等三角形的判定定理可得△BAE≌△DAC,由全等三角形的性质可得BE=DC,∠BEA=∠DCA,设AE与CD相交于点F,易得
∠BEA+∠DFE=90°.即CD⊥BE.
解:CD=BE,CD⊥BE,
理由如下:
因为∠BAD=∠CAE=90°,所以∠BAD+∠DAE=∠CAE+∠DAE,
即∠BAE=∠DAC.
因为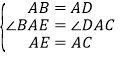 ,
,
所以△BAE≌△DAC(SAS).
所以BE=DC,∠BEA=∠DCA.
如图,设AE与CD相交于点F,因为∠ACF+∠AFC=90°,∠AFC=∠DFE,
所以∠BEA+∠DFE=90°.即CD⊥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“父母恩深重,恩怜无歇时”,每年5月的第二个星期日即为母亲节,节日前夕巴蜀中学学生会计划采购一批鲜花礼盒赠送给妈妈们.
(1)经过和花店卖家议价,可在原标价的基础上打八折购进,若在花店购买80个礼盒最多花费7680元,请求出每个礼盒在花店的最高标价;(用不等式解答)
(2)后来学生会了解到通过“大众点评”或“美团”同城配送会在(1)中花店最高售价的基础上降价25%,学生会计划在这两个网站上分别购买相同数量的礼盒,但实际购买过程中,“大众点评”网上的购买价格比原有价格上涨 m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了
m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了 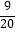 m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了
m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了 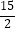 m%,求出m的值.
m%,求出m的值. -
科目: 来源: 题型:
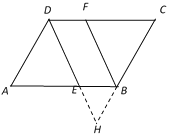
查看答案和解析>>【题目】如图,直线AD∥BC,E,F分别在线段AB,CD上,∠ADE=∠FBC,判断直线DE与BF的位置关系,以下是解答过程,请补充完整,其中括号里填依据.
解:DE∥BF.
理由如下:延长DE交CB延长线于H点,
因为AD∥BC(__________).
所以∠ADE=∠H(__________).
又因为∠ADE=∠FBC(已知),
所以______=______(________).
所以DE∥BF(___________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.
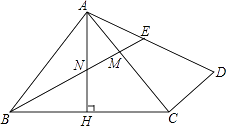
(1)若AB=3,AD=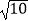 ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD=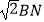 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于点E,连接AD,则下列结论正确的个数是( )
①AD⊥BC;②∠EDA=∠B;③OA= AC;④DE是⊙O的切线.
AC;④DE是⊙O的切线.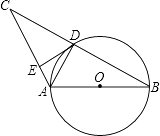
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计,并绘制如图所示的扇形统计图和条形统计图.根据图中信息解答下列问题:
(1)该超市“元旦”期间共销售 个绿色鸡蛋,A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是 度;
(2)补全条形统计图;
(3)如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个,请你估计这个分店销售的B种品牌的绿色鸡蛋的个数?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在四川汶川地震灾后重建中,某公司拟为灾区援建一所希望学校.公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的1.5倍,甲、乙两队合作完成建校工程需要72天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)在施工过程中,该公司派一名技术人员在现场对施工质量进行全程监督,每天需要补助100元.若由甲工程队单独施工时平均每天的费用为0.8万元.现公司选择了乙工程队,要求其施工总费用不能超过甲工程队,则乙工程队单独施工时平均每天的费用最多为多少?
相关试题

