【题目】“父母恩深重,恩怜无歇时”,每年5月的第二个星期日即为母亲节,节日前夕巴蜀中学学生会计划采购一批鲜花礼盒赠送给妈妈们.
(1)经过和花店卖家议价,可在原标价的基础上打八折购进,若在花店购买80个礼盒最多花费7680元,请求出每个礼盒在花店的最高标价;(用不等式解答)
(2)后来学生会了解到通过“大众点评”或“美团”同城配送会在(1)中花店最高售价的基础上降价25%,学生会计划在这两个网站上分别购买相同数量的礼盒,但实际购买过程中,“大众点评”网上的购买价格比原有价格上涨 ![]() m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了
m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了 ![]() m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了
m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了 ![]() m%,求出m的值.
m%,求出m的值.
参考答案:
【答案】
(1)解:解法一:设标价为x元,
列不等式为0.8x80≤7680,
x≤120;
解法二:7680÷80÷0.8,
=96÷0.8,
=120(元),
答:每个礼盒在花店的最高标价是120元;
(2)解:假设学生会计划在这两个网站上分别购买的礼盒数为a个礼盒,
由题意得:120×0.8a(1﹣25%)(1+ ![]() m%)+a[120×0.8(1﹣25%)﹣
m%)+a[120×0.8(1﹣25%)﹣ ![]() m](1+15m%)=120×0.8a(1﹣25%)×2(1+
m](1+15m%)=120×0.8a(1﹣25%)×2(1+ ![]() m%),
m%),
72a(1+ ![]() m%)+a(72﹣
m%)+a(72﹣ ![]() m)(1+15m%)=144a(1+
m)(1+15m%)=144a(1+ ![]() m%),
m%),
0.0675m2﹣1.35m=0,
m2﹣20m=0
m1=0(舍),m2=20,
答:m的值是20.
【解析】(1)方法一:可以设:设标价为x元,列不等式为0.8x80≤7680,即可解决问题;方法二:根据单价=总价![]() 数量先求出一个礼盒最多花费,再除以折扣可求出每个礼盒在花店的最高标价;
数量先求出一个礼盒最多花费,再除以折扣可求出每个礼盒在花店的最高标价;
(2)假设学生会计划在这两个网站上分别购买的礼盒数为a个礼盒,表示在大众点评网上的购买实际消费总额以及在美团网上的购买实际消费总额,根据在两个网站的实际消费总额比原计划的预算总额增加了![]() m%,列方程解出即可。
m%,列方程解出即可。
【考点精析】本题主要考查了一元一次不等式组的应用的相关知识点,需要掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
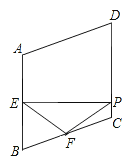
A. 35° B. 45° C. 50° D. 55°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a个单位到△DEF的位置.
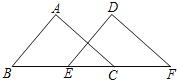
(1)当△ABC所扫过的面积为32时,求a的值;
(2)连接AE、AD,当AB=5,a=5时,试判断△ADE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=﹣
 (x﹣h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=
(x﹣h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=  x+
x+  经过点A与对称轴交于E,点E的纵坐标为3.
经过点A与对称轴交于E,点E的纵坐标为3.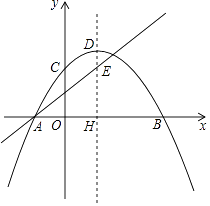
(1)求h、k的值;
(2)点P为第四象限抛物线上一点,连接PH,点Q为PH的中点,连接AQ、AP,设点P的横坐标为t,△AQP的面积为S,求S与t的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,过点Q作y轴的平行线QK,过点D作y轴的垂直DK,直线QK、DK交于点K,连接PK、EK,若2∠DKE+∠HPK=90°,求点P的横坐标. -
科目: 来源: 题型:
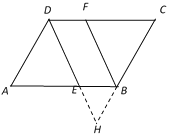
查看答案和解析>>【题目】如图,直线AD∥BC,E,F分别在线段AB,CD上,∠ADE=∠FBC,判断直线DE与BF的位置关系,以下是解答过程,请补充完整,其中括号里填依据.
解:DE∥BF.
理由如下:延长DE交CB延长线于H点,
因为AD∥BC(__________).
所以∠ADE=∠H(__________).
又因为∠ADE=∠FBC(已知),
所以______=______(________).
所以DE∥BF(___________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.
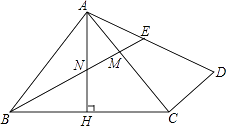
(1)若AB=3,AD=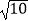 ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD=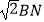 .
. -
科目: 来源: 题型:
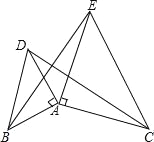
查看答案和解析>>【题目】如图,已知AB=AD,AC=AE,∠BAD=∠CAE=90°,试判断CD与BE的大小关系和位置关系,并进行证明.
相关试题

