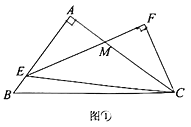
【题目】已知,在![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,以
上一动点,以![]() 为斜边作
为斜边作![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,且
,且![]() .
.
(1)如图①,若![]() 平分
平分![]() ,
,![]() ,求
,求![]() 的长
的长
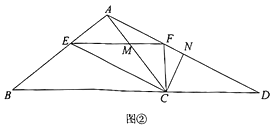
(2)如图②,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,求证
,求证![]() .
.
参考答案:
【答案】(1)12;(2)见解析
【解析】
(1)由“SAS”可证△AEM≌△FCM,可得EM=MC,由等腰三角形性质可求∠AEF=∠MCE=∠MEC=30°,由直角三角形的性质可求ME=MC=8,即可求AC的长;
(2)过点C作CG⊥AC交AD于点G,由“SAS”可证△ACG≌△EFC,可得AG=CE,CF=CG,由等腰三角形的性质可得FG=2FN,即可得结论.
(1)∵EF平分∠AEC,
∴∠AEF=∠FEC,
∵∠BAC=∠EFC=90°,AM=MF,∠AME=∠FMC
∴△AEM≌△FCM(SAS)
∴EM=MC
∴∠MEC=∠MCE
∴∠MEC=∠MCE=∠AEF,
∵∠MEC+∠MCE+∠AEF=90°
∴∠AEF=∠MCE=∠MEC=30°,且∠BAC=90°
∴EM=2AM=8
∴MC=8
∴AC=AM+MC=12
(2)如图,过点C作CG⊥AC交AD于点G,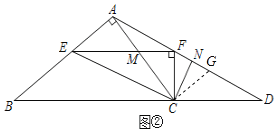
由(1)可知:EM=MC
∵AM=MF
∴AC=EF,
∵∠BAC=∠EFC=90°
∴点A,点F,点C,点E四点共圆
∴∠CAG=∠FEC,且AC=EF,∠EFC=∠ACG=90°
∴△ACG≌△EFC(ASA)
∴AG=CE,CF=CG,
∵CF=CG,CN⊥AG
∴FG=2FN
∴EC=AG=AF+FG=AF+2FN
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将平行四边形 ABCD 沿对角线 BD 折叠,使点 A 落在A′处,若∠1=∠2=50°,则∠A′的度数为( )

A.100°B.105°C.110°D.115°
-
科目: 来源: 题型:
查看答案和解析>>【题目】对两实数
 ,
, 定义一种新运算,规定
定义一种新运算,规定 .
.例如:
 .
.(1)填空:
 ________;
________; ________.
________.(2)若
 ,求
,求 的值.
的值.(3)若
 ,
, 为整数,且
为整数,且 ,求满足条件的所有
,求满足条件的所有 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形
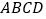 中,
中,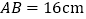 ,
,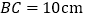 ,动点
,动点 从
从 出发,匀速沿
出发,匀速沿 运动,到点
运动,到点 停止;同时动点
停止;同时动点 从
从 出发,匀速沿
出发,匀速沿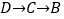 运动,速度是动点
运动,速度是动点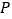 速度的一半,当其中一个点到达终点时,另一个点停止运动.如图②是点
速度的一半,当其中一个点到达终点时,另一个点停止运动.如图②是点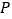 出发后
出发后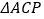 的面积
的面积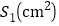 与运动时间
与运动时间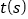 之间的关系图象.
之间的关系图象.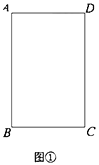
(1)图②中,求
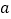 ,
, 的值.
的值.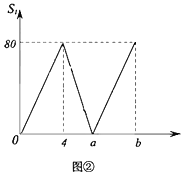
(2)当
 运动多少秒后,
运动多少秒后, ,
,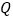 两点相遇.
两点相遇.(3)在点
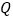 从点
从点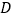 运动到点
运动到点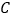 的过程中,记点
的过程中,记点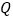 出发后
出发后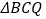 的面积为
的面积为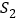 ,当
,当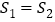 ,时,求动点
,时,求动点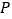 运动的时间
运动的时间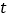 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于二次函数y=ax2+bx+c的图象有下列命题:
①当c=0时,函数的图象经过原点;
②当c>0,且函数的图象开口向下时,方程ax2+bx+c=0必有两个不相等的实根;
③函数图象最高点的纵坐标是
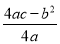 ;
;④当b=0时,函数的图象关于y轴对称.
其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=
 ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是__.
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图平行四边形 ABCD 中,∠ABC=60°,点 E、F 分别在 CD、BC 的延长线上,AE∥BD,EF⊥BF,垂足为点 F,DF=2.

(1)求证:D 是 EC 中点;
(2)求 FC 的长.
相关试题

