【题目】如图平行四边形 ABCD 中,∠ABC=60°,点 E、F 分别在 CD、BC 的延长线上,AE∥BD,EF⊥BF,垂足为点 F,DF=2.

(1)求证:D 是 EC 中点;
(2)求 FC 的长.
参考答案:
【答案】(1)见解析;(2)2
【解析】
(1)根据平行四边形的对边平行可以得到AB∥CD,又AE∥BD,可以证明四边形ABDE是平行四边形,所以AB=DE,故D是EC的中点;
(2)连接EF,则△EFC是直角三角形,根据直角三角形斜边上的中线等于斜边的一半可以得到△CDF是等腰三角形,再利用∠ABC=60°推得∠DCF=60°,所以△CDF是等边三角形,FC=DF,FC的长度即可求出.
(1)在平行四边形ABCD中,
AB∥CD,且AB=CD,
又∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴CD=DE,
即D是EC的中点;
(2)连接EF,

∵EF⊥BF,
∴△EFC是直角三角形,
又∵D是EC的中点,
∴DF=CD=DE=2,
在平行四边形ABCD中,AB∥CD,
∵∠ABC=60°,
∴∠ECF=∠ABC=60°,
∴△CDF是等边三角形,
∴FC=DF=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在
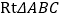 中,
中,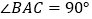 ,
,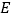 为
为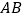 上一动点,以
上一动点,以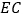 为斜边作
为斜边作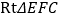 ,
,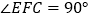 ,
,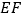 交
交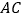 于点
于点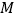 ,且
,且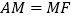 .
.(1)如图①,若
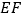 平分
平分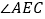 ,
,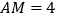 ,求
,求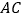 的长
的长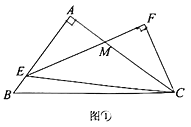
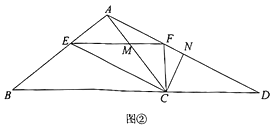
(2)如图②,连接
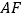 并延长交
并延长交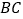 的延长线于点
的延长线于点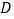 ,过点
,过点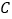 作
作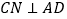 于
于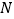 ,求证
,求证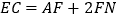 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于二次函数y=ax2+bx+c的图象有下列命题:
①当c=0时,函数的图象经过原点;
②当c>0,且函数的图象开口向下时,方程ax2+bx+c=0必有两个不相等的实根;
③函数图象最高点的纵坐标是
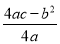 ;
;④当b=0时,函数的图象关于y轴对称.
其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=
 ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是__.
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形
 中,
中, 是线段
是线段 上一点,
上一点, 是
是 延长线上一点.连接
延长线上一点.连接 ,
, .点
.点 是线段
是线段 的中点,
的中点, ,
, 与
与 延长线交于点
延长线交于点 .
.
(1)若
 ,求
,求 ;
;(2)若
 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
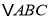 三个顶点的坐标分别为
三个顶点的坐标分别为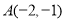 ,
,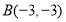 ,
,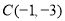 ,
,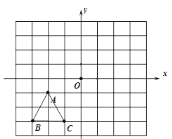
(1)若将△ABC 向右平移三个单位长度得到△A1B1C1,则点 A1 的坐标为________

(2)若△ABC 与△A2B2C2 关于原点 O 成中心对称,则点 A2 的坐标________;
(3)画出△ABC 绕原点 O 顺时针旋转 90°后的对应图形△A3B3C3,并写出 A3 的坐标_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

