搜索
【题目】如图,将一根绳子对折以后用线段
表示,现从
处将绳子剪断,剪断后的各段绳子中最长的一段为
，若
，则这条绳子的原长为（ ）
A.
B.
C.
D.
参考答案：
【答案】C
【解析】
设AP＝2xcm，则BP＝3xcm，分为两种情况：①当含有线段AP的绳子最长时，得出方程2x＋2x＝60，②当含有线段BP的绳子最长时，得出方程3x＋3x＝60，求出每个方程的解，代入2（3x＋2x）求出即可．
设AP＝2xcm，则BP＝3xcm，①当含有线段AP的绳子最长时，2x＋2x＝60，解得：x＝15，即绳子的原长是2（2x＋3x）＝10x＝150（cm）；②当含有线段BP的绳子最长时，3x＋3x＝60，解得：x＝10，即绳子的原长是2（2x＋3x）＝10x＝100（cm）；故答案为100cm或150cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一条直路上的
、
、
、
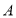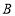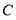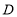四个车站的位置如图所示（单位千米），如果小明家在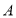站旁，他的同学小亮家在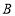站旁，新华书店在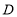站旁，一天小明乘车从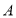站出发到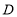站下车去新华书店购买一些课外阅读书籍，途径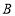、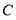两站，当小明到达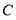站时发现自己所带钱不够购买自己所要的书籍.于是他乘车返回到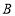站处下车向小亮借足了钱，然后乘车继续赶往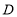站旁的新华书店.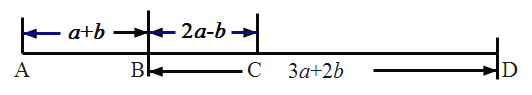
（1）求
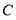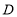、两站的距离；（用含有
、
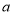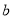的代数式表示）（2）求这一天小明从
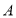站到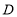站乘车路程.（用含有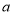、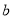的代数式表示） -
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数y1=x+m的图象与反比例函数
的图象交于A、B两点．已知当x＞1时，y1＞y2；当0＜x＜1时，y1＜y2．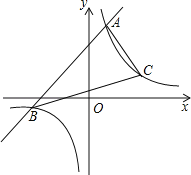
（1）求一次函数的解析式；
（2）已知双曲线在第一象限上有一点C到y轴的距离为3，求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校教学楼（甲楼）的顶部E和大门A之间挂了一些彩旗．小颖测得大门A距甲楼的距离AB是31cm，在A处测得甲楼顶部E处的仰角是31°．
（1）求甲楼的高度及彩旗的长度；（精确到0.01m）
（2）若小颖在甲楼楼底C处测得学校后面医院楼（乙楼）楼顶G处的仰角为40°，爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为19°，求乙楼的高度及甲乙两楼之间的距离．（精确到0.01m）
（cos31°≈0.86，tan31°≈0.60，cos19°≈0.95，tan19°≈0.34，cos40°≈0.77，tan40°≈0.84）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过
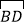上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．（1）求证：△ECF∽△GCE；
（2）求证：EG是⊙O的切线；
（3）延长AB交GE的延长线于点M，若tanG=
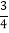，AH=3
，求EM的值．
-
科目： 来源： 题型：
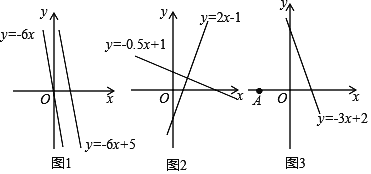
查看答案和解析>>【题目】材料一：如图1，由课本91页例2画函数y＝﹣6x与y＝﹣6x+5可知，直线y＝﹣6x+5可以由直线y＝﹣6x向上平移5个单位长度得到由此我们得到正确的结论一：在直线L1：y=K1x+b1与直线L2：y=K2x+b2中，如果K1=K2 且b1≠b2 ，那么L1∥L2，反过来，也成立．
材料二：如图2，由课本92页例3画函数y＝2x﹣1与y＝﹣0.5x+1可知，利用所学知识一定能证出这两条直线是互相垂直的．由此我们得到正确的结论二：在直线L1：y=k1x+b1 与L2：y=k2x+b2 中，如果k1·k2=-1那么L1⊥L2，反过来，也成立
应用举例
已知直线y＝﹣
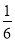x+5与直线y＝kx+2互相垂直，则﹣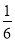k＝﹣1．所以k＝6解决问题
(1)请写出一条直线解析式______，使它与直线y＝x﹣3平行．
(2)如图3，点A坐标为(﹣1，0)，点P是直线y＝﹣3x+2上一动点，当点P运动到何位置时，线段PA的长度最小？并求出此时点P的坐标．
-
科目： 来源： 题型：
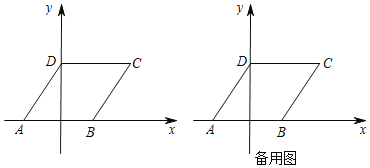
查看答案和解析>>【题目】如图，ABCD在平面直角坐标系中，点A（﹣2，0），点B（2，0），点D（0，3），点C在第一象限．
（1）求直线AD的解析式；
（2）若E为y轴上的点，求△EBC周长的最小值；
（3）若点Q在平面直角坐标系内，点P在直线AD上，是否存在以DP，DB为邻边的菱形DBQP？若存在，求出点P的坐标；若不存在，请说明理由．
相关试题
