【题目】已知一次函数y1=x+m的图象与反比例函数![]() 的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
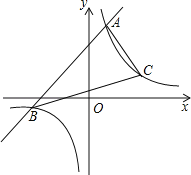
(1)求一次函数的解析式;
(2)已知双曲线在第一象限上有一点C到y轴的距离为3,求△ABC的面积.
参考答案:
【答案】(1)y1=x+5 (2)21
【解析】
试题分析:(1)首先根据x>1时,y1>y2,0<x<1时,y1<y2确定点A的横坐标,然后代入反比例函数解析式求出点A的纵坐标,从而得到点A的坐标,再利用待定系数法求直线解析式解答;
(2)根据点C到y轴的距离判断出点C的横坐标,代入反比例函数解析式求出纵坐标,从而得到点C的坐标,过点C作CD∥x轴交直线AB于D,求出点D的坐标,然后得到CD的长度,再联立一次函数与双曲线解析式求出点B的坐标,然后△ABC的面积=△ACD的面积+△BCD的面积,列式进行计算即可得解.
解:(1)∵当x>1时,y1>y2;当0<x<1时,y1<y2,
∴点A的横坐标为1,
代入反比例函数解析式,![]() =y,
=y,
解得y=6,
∴点A的坐标为(1,6),
又∵点A在一次函数图象上,
∴1+m=6,
解得m=5,
∴一次函数的解析式为y1=x+5;
(2)∵第一象限内点C到y轴的距离为3,
∴点C的横坐标为3,
∴y=![]() =2,
=2,
∴点C的坐标为(3,2),
过点C作CD∥x轴交直线AB于D,
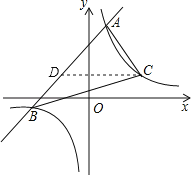
则点D的纵坐标为2,
∴x+5=2,
解得x=﹣3,
∴点D的坐标为(﹣3,2),
∴CD=3﹣(﹣3)=3+3=6,
点A到CD的距离为6﹣2=4,
联立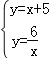 ,
,
解得![]() (舍去),
(舍去),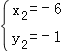 ,
,
∴点B的坐标为(﹣6,﹣1),
∴点B到CD的距离为2﹣(﹣1)=2+1=3,
S△ABC=S△ACD+S△BCD=![]() ×6×4+
×6×4+![]() ×6×3=12+9=21.
×6×3=12+9=21.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|
当A、B两点中有一点在原点时,不妨设点A在原点(如图1)|AB|=|OB|=|b|=|a﹣b|;
当A、B两点都不在原点时
①当点A、B都在原点的右边(如图2)
|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
②当点A、B都在原点的左边(如图3)
|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|
③当点A、B在原点的两边(如图4)
|AB|=|OB|+|OA|=|b|+|a|=﹣b+a=|a﹣b|
回答下列问题:
(1)数轴上表示1和5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是﹣2,则点A和B之间的距离是 ,若|AB|=3,那么x为 ;
(3)当x是 时,代数式|x+2|+|x﹣1|=5;
(4)若点A表示的数﹣1,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒
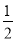 个单位长度,求运动几秒后,点Q与点P相距1个单位?(请写出必要的求解过程)
个单位长度,求运动几秒后,点Q与点P相距1个单位?(请写出必要的求解过程)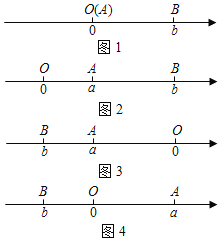
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,线段AB上有两个点C、D,请计算图中共有多少条线段?

(2)如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?
(3)拓展应用:8个班级参加学校组织的篮球比赛,比赛采用单循环制(即每两个班级之间都要进行一场比赛),那么一共要进行多少场比赛?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条直路上的
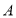 、
、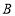 、
、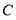 、
、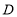 四个车站的位置如图所示(单位千米),如果小明家在
四个车站的位置如图所示(单位千米),如果小明家在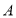 站旁,他的同学小亮家在
站旁,他的同学小亮家在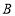 站旁,新华书店在
站旁,新华书店在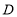 站旁,一天小明乘车从
站旁,一天小明乘车从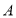 站出发到
站出发到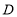 站下车去新华书店购买一些课外阅读书籍,途径
站下车去新华书店购买一些课外阅读书籍,途径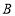 、
、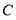 两站,当小明到达
两站,当小明到达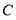 站时发现自己所带钱不够购买自己所要的书籍.于是他乘车返回到
站时发现自己所带钱不够购买自己所要的书籍.于是他乘车返回到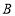 站处下车向小亮借足了钱,然后乘车继续赶往
站处下车向小亮借足了钱,然后乘车继续赶往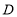 站旁的新华书店.
站旁的新华书店.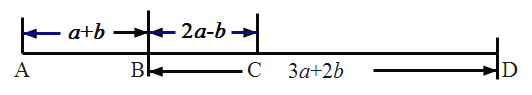
(1)求
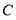 、
、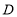 两站的距离;(用含有
两站的距离;(用含有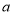 、
、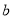 的代数式表示)
的代数式表示)(2)求这一天小明从
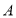 站到
站到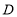 站乘车路程.(用含有
站乘车路程.(用含有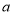 、
、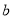 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校教学楼(甲楼)的顶部E和大门A之间挂了一些彩旗.小颖测得大门A距甲楼的距离AB是31cm,在A处测得甲楼顶部E处的仰角是31°.
(1)求甲楼的高度及彩旗的长度;(精确到0.01m)
(2)若小颖在甲楼楼底C处测得学校后面医院楼(乙楼)楼顶G处的仰角为40°,爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为19°,求乙楼的高度及甲乙两楼之间的距离.(精确到0.01m)
(cos31°≈0.86,tan31°≈0.60,cos19°≈0.95,tan19°≈0.34,cos40°≈0.77,tan40°≈0.84)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一根绳子对折以后用线段
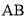 表示,现从
表示,现从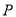 处将绳子剪断,剪断后的各段绳子中最长的一段为
处将绳子剪断,剪断后的各段绳子中最长的一段为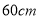 ,若
,若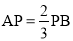 ,则这条绳子的原长为( )
,则这条绳子的原长为( )
A.
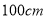 B.
B.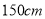 C.
C.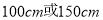 D.
D.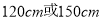
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过
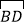 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=
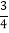 ,AH=3
,AH=3 ,求EM的值.
,求EM的值.
相关试题

