【题目】如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,以线段
,以线段![]() 为边在第一象限内作等腰直角三角形
为边在第一象限内作等腰直角三角形![]() ,使
,使![]() .
.
(1)分别求点![]() 的坐标;
的坐标;
(2)在![]() 轴上求一点
轴上求一点![]() ,使它到
,使它到![]() 两点的距离之和最小.
两点的距离之和最小.

参考答案:
【答案】(1) B的坐标是(0,2),C的坐标是(5,3);(2) P(2,0).
【解析】
(1)先根据一次函数的解析式求出A、B两点的坐标,再作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,故可得出C点坐标;
(2)求得B点关于x轴的对称点B'的坐标,连接B'C与x轴的交点即为所求的P点,由B'、C坐标可求得直线B'C的解析式,则可求得P点坐标.
解:∵一次函数![]() 中,令x=0得:y=2;
中,令x=0得:y=2;
令y=0,解得x=3.
∴B的坐标是(0,2),A的坐标是(3,0).
作CD⊥x轴于点D.
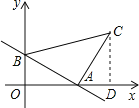
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO,
又∵AB=AC,∠BOA=∠CDA=90°,
∴△ABO≌△CAD(AAS),
∴AD=OB=2,CD=OA=3,OD=OA+AD=5.
则C的坐标是(5,3).
(2)如图,作点B关于x轴的对称点B',连接CB'交x轴于P,此时PB+PC的值最小.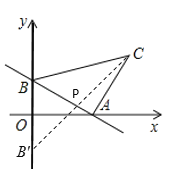
∵B(0,2),C(5,3)
∴B'(0,-2),
设直线C B'的解析式为y=kx+b,
把(0,-2) (5,3)代入y=kx+b中,
可得:![]() ,
,
解得:![]() ,
,
∴直线CB'的解析式为y=x-2,
令y=0,得到x=2,
∴P(2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.

(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2 ,求阴影部分的面积.
,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 分别为边
分别为边 的中点,
的中点, 是对角线,过点
是对角线,过点 作
作 交
交 的延长线于点
的延长线于点 .
.(1)求证:
 ;
;(2)若
 ,求证:四边形
,求证:四边形 是菱形.
是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校利用五一组织老师去娄山关进行红色文化拓展活动,现有甲、乙两家旅行 社可供选择,票价都是
 元/人,甲旅行社的优惠方案是:按总价打八五折;乙旅行社 的优惠方案是:前
元/人,甲旅行社的优惠方案是:按总价打八五折;乙旅行社 的优惠方案是:前 人按原价付费,超过的部分
人按原价付费,超过的部分 折优惠.该校有教师
折优惠.该校有教师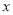 人.
人. (1)设总价为
 元.写出
元.写出 与
与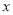 之间的函数关系式;
之间的函数关系式; (2)在不晓得该校人数的情况下,请给学校提出比较省钱的购票建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两个工程队共同修建一条公路,从两端同时开始,到工程结束时,甲工程 队共施工了
 天,乙队在中途接到紧急任务停止施工一段时间,回来后按照以前的施工 速度继续施工至结束,设甲、乙两工程队各自施工的长度分別为
天,乙队在中途接到紧急任务停止施工一段时间,回来后按照以前的施工 速度继续施工至结束,设甲、乙两工程队各自施工的长度分別为 (米),
(米), (米),甲 队施工的时间为
(米),甲 队施工的时间为 (天),
(天), ,
, 与
与 之间的函数图象如图所示.
之间的函数图象如图所示.(1)这条公路的总长度是______米;
(2)求乙队在恢复施工后,
 与
与 之间的函数表 达式;
之间的函数表 达式;(3)求在修建该条公路的过程中,甲、乙两队共同修建完
 米长时甲队施工的天数.
米长时甲队施工的天数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.

(1)求证:△ACD∽△BAD;
(2)求证:AD是⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.

(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.
相关试题

