搜索
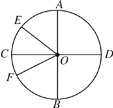
【题目】如图，圆O的直径为10 cm，两条直径AB，CD相交成90°角，∠AOE＝50°，OF是∠BOE的平分线．
(1)求圆心角∠COF的度数；
(2)求扇形COF的面积．
参考答案：
【答案】(1)25°;(2)
cm.
【解析】
(1)由已知可得∠AOB=180°，求出∠BOE=130°.由OF是∠BOE的平分线，得∠BOF=∠BOE=65°，由直角定义得∠COF=90°－65°=25°.
(2)扇形COF的面积=25π×
=
π(cm2)．
解：(1)∵∠AOB=180°，∠AOE=50°，
∴∠BOE=130°.
∵OF是∠BOE的平分线，
∴∠BOF=
∠BOE=65°.
∵两条直径AB，CD相交成90°角，
∴∠COF=90°－65°=25°.
(2)∵⊙O的面积=52×π=25π，
∴扇形COF的面积=25π×=π(cm2)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，C，D是线段AB上的两点，已知AC：CD：DB=1：2：3，MN分别是AC，BD的中点，且AB=36cm，求线段MN的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是两个可以自由转动的转盘，转盘A被分成三个面积相等的扇形，转盘B被分成两个面积相等的扇形．
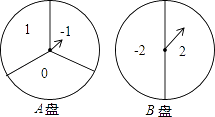
（1）转动转盘A一次，所得到的数字是负数的概率为
（2）转动两个转盘各一次，请用列表法或画树状图法求所得到的数字均是负数的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，直线y=--
x＋8与x轴，y轴分别交于点A，点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．(1)求AB的长和点C的坐标；
(2)求直线CD的表达式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】2015年深圳国际马拉松赛于12月7日拉开帷幕，某马拉松爱好者用无人机拍摄比赛过程．如图，在无人机的镜头C下，观测深南大道A处的俯角为30°，B处的俯角为45°．如果此时无人机镜头C处离路面的高度CD为100米，点A、D、B在同一直线上，求A、B两处之间的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知菱形ABCD中，AB=6，∠B=60°．E是BC边上一动点，F是CD边上一动点，且BE=CF，连接AE、AF．
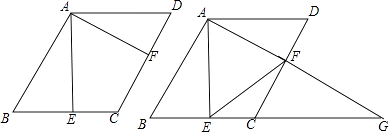
（1）∠EAF的度数是；
（2）求证：AE=AF；
（3）延长AF交BC的延长线于点G，连接EF，设BE=x，EF2=y，求y与x之间的函数关系式． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知直线l：y=﹣x+2与x轴交于点A、与y轴交于点B．抛物线y=ax2+bx+c（a≠0）经过O、A两点，与直线l交于点C，点C的横坐标为﹣1．
（1）求该抛物线的函数表达式；
（2）若点P是位于直线l下方抛物线上的一个动点，且不与点A、点C重合，连接PA、PC．设△PAC的面积为S，求当S取得最大值时点P的坐标，并求S的最大值；
（3）如图2，设抛物线的顶点为D，连接AD、BD．点E是对称轴m上一点，F是抛物线上一点，请直接写出当△DEF与△ABD相似时点E的坐标．
相关试题
