【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E.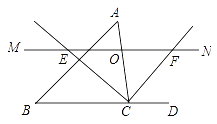
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论;
(3)在(2)的条件下,试猜想当△ABC满足什么条件时使四边形AECF是正方形,请直接写出你的结论.
参考答案:
【答案】
(1)
证明:如图1中,
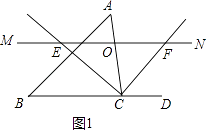
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠OEC=∠ECB,
∴∠OEC=∠OCE,
∴OE=OC,
同理,OC=OF,
∴OE=OF.
(2)
结论:当点O运动到AC中点处时,四边形AECF是矩形.
理由:如图2中,
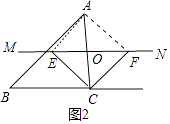
如图AO=CO,EO=FO,
∴四边形AECF为平行四边形,
∵CE平分∠ACB,
∴∠ACE= ![]() ∠ACB,
∠ACB,
同理,∠ACF= ![]() ∠ACG,
∠ACG,
∴∠ECF=∠ACE+∠ACF= ![]() (∠ACB+∠ACG)=
(∠ACB+∠ACG)= ![]() ×180°=90°,
×180°=90°,
∴四边形AECF是矩形.:
(3)
解:结论:当∠ACB=90°时,四边形AECF是正方形
理由:∵∠BCA=90°,
∵MN∥BC,
∴∠BCA=∠AOM=90°,
∴AC⊥EF,
∴四边形AECF是正方形..
【解析】(1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.(3)利用已知条件及正方形的判定方法解答.
【考点精析】解答此题的关键在于理解正方形的判定方法的相关知识,掌握先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形纸片的AB边在y轴上,BC边在x轴上,B与坐标原点重合,折叠长方形ABCD的一边AD,使点D落在BC边的F处,折痕为AE,已知A点坐标为(0,8),C点坐标为(10,0). 求:E点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.

(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若b反射出的光线n平行于m,且∠1=50°,则∠2= , ∠3=;
(2)在(1)中,若∠1=40°,则∠3= , 若∠1=55°,则∠3=;
(3)由(1)(2)请你猜想:当∠3=时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由. -
科目: 来源: 题型:
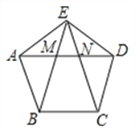
查看答案和解析>>【题目】如图,正五边形的边长为2,连对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,则MN=__________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=﹣1是方程2x+a=0的解,则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(m,1﹣2m)的横坐标与纵坐标互为相反数,则点P一定在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】用一元一次方程解下列应用题
据国家统计局发布的数据显示,在我国的664个城市中,按水资源可分为暂不缺水城市、一般缺水城市和严重缺水城市三类.其中,暂不缺水城市比严重缺水城市的4倍少50个,一般缺水城市是严重缺水城市的2倍.
(1)求严重缺水城市有多少个?
(2)为了解决缺水的问题,国家启动了多个水利工程,缓解了部分严重缺水城市的情况,使一般性缺水城市的数目是严重缺水城市的9倍,求现在一般性缺水的城市有多少个?
相关试题

