【题目】如图,在平面直角坐标系中,长方形纸片的AB边在y轴上,BC边在x轴上,B与坐标原点重合,折叠长方形ABCD的一边AD,使点D落在BC边的F处,折痕为AE,已知A点坐标为(0,8),C点坐标为(10,0). 求:E点坐标.
参考答案:
【答案】解:∵四边形ABCD为矩形,点B与点O重合, ∴DC=AB=8cm,AF=AD=BC=10.
设EF=DE=xcm,EC=8﹣x;
由勾股定理得:BF2=102﹣82 ,
∴BF=6,
∴CF=10﹣6=4;
在Rt△EFC中,由勾股定理得:x2=42+(8﹣x)2 ,
解得:x=5,
EC=8﹣5=3.
∴E点的坐标为(10,3).
【解析】根据勾股定理求出BF的长;进而求出FC的长度;由题意得EF=DE;利用勾股定理列出关于EC的方程,解方程即可解决问题.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强用8块棱长为3 cm的小正方体,搭建了一个如图所示的积木,下列说法中不正确的是( )
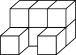
A. 从左面看这个积木时,看到的图形面积是27cm2
B. 从正面看这个积木时,看到的图形面积是54cm2
C. 从上面看这个积木时,看到的图形面积是45cm2
D. 分别从正面、左面、上面看这个积木时,看到的图形面积都是72cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,点E,F在对角线BD上,且BE=DF,求证:
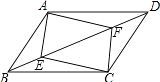
(1)AE=CF;
(2)四边形AECF是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=
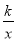 (k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )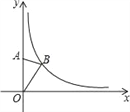
A. 逐渐减小 B. 逐渐增大 C. 先增大后减小 D. 不变
-
科目: 来源: 题型:
查看答案和解析>>【题目】科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.

(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若b反射出的光线n平行于m,且∠1=50°,则∠2= , ∠3=;
(2)在(1)中,若∠1=40°,则∠3= , 若∠1=55°,则∠3=;
(3)由(1)(2)请你猜想:当∠3=时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形的边长为2,连对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,则MN=__________;
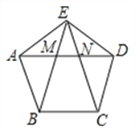
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E.
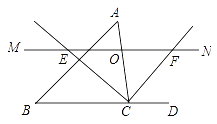
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论;
(3)在(2)的条件下,试猜想当△ABC满足什么条件时使四边形AECF是正方形,请直接写出你的结论.
相关试题

