【题目】某中学学生步行到郊外旅行,七年级![]() 班学生组成前队,步行速度为4千米
班学生组成前队,步行速度为4千米![]() 小时,七
小时,七![]() 班的学生组成后队,速度为6千米
班的学生组成后队,速度为6千米![]() 小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米
小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米![]() 小时.
小时.
![]() 后队追上前队需要多长时间?
后队追上前队需要多长时间?
![]() 后队追上前队的时间内,联络员走的路程是多少?
后队追上前队的时间内,联络员走的路程是多少?
![]() 七年级
七年级![]() 班出发多少小时后两队相距2千米?
班出发多少小时后两队相距2千米?
参考答案:
【答案】(1)后队追上前队需要2小时;(2)联络员走的路程是20千米;(3)七年级![]() 班出发
班出发![]() 小时或2小时或4小时后,两队相距2千米
小时或2小时或4小时后,两队相距2千米
【解析】
(1) 设后队追上前队需要x小时,由后队走的路程=前队先走的路程+前队后来走的路程,列出方程,求解即可;
(2)由路程=速度×时间可求联络员走的路程;
(3)分三种情况讨论,列出方程求解即可.
![]() 设后队追上前队需要x小时,
设后队追上前队需要x小时,
根据题意得:![]()
![]() ,
,
答:后队追上前队需要2小时;
![]() 千米,
千米,
答:联络员走的路程是20千米;
![]() 设七年级
设七年级![]() 班出发t小时后,两队相距2千米,
班出发t小时后,两队相距2千米,
当七年级![]() 班没有出发时,
班没有出发时,![]() ,
,
当七年级![]() 班出发,但没有追上七年级
班出发,但没有追上七年级![]() 班时,
班时,![]() ,
,
![]() ,
,
当七年级![]() 班追上七年级
班追上七年级![]() 班后,
班后,![]() ,
,
![]() ,
,
答:七年级![]() 班出发
班出发![]() 小时或2小时或4小时后,两队相距2千米.
小时或2小时或4小时后,两队相距2千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“
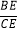 =x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).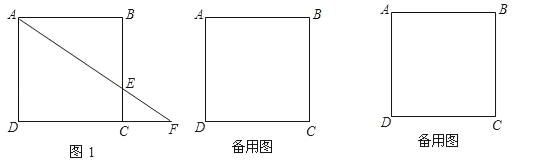
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的四个顶点分别在反比例函数
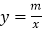 与
与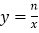 (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以点O为端点按顺时针方向依次作射线OA、OB、OC、OD.
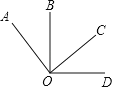
(1)若∠AOC、∠BOD都是直角,∠BOC=60°,求∠AOB和∠DOC的度数.
(2)若∠BOD=100°,∠AOC=110°,且∠AOD=∠BOC+70°,求∠COD的度数.
(3)若∠AOC=∠BOD=α,当α为多少度时,∠AOD和∠BOC互余?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距
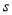 (米),甲行走的时间为
(米),甲行走的时间为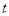 (分),
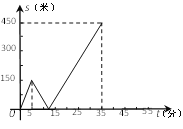
(分),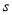 关于
关于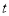 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.(1)求甲行走的速度;
(2)在坐标系中,补画
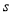 关于
关于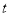 函数图象的其余部分;
函数图象的其余部分;(3)问甲、乙两人何时相距360米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=
 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
A. 3 B. 4 C. 5 D. 4

-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
相关试题

