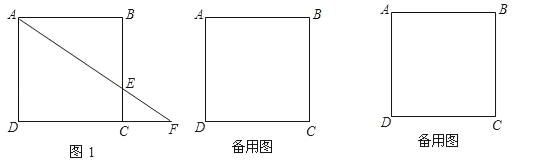
【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“![]() =x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
参考答案:
【答案】(1)![]() ;(2) ①
;(2) ①![]() , ②
, ②![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)利用平行线性质以及线段比求出CF的值;
(2)本题要分两种方法讨论:①若点E在线段BC上;②若点E在边BC的延长线上.需运用勾股定理求出与之相联的线段;
(3)本题分两种情况讨论:若点E在线段BC上,y=![]() ,自变量取值范围为x>0;若点E在边BC的延长线上,y=
,自变量取值范围为x>0;若点E在边BC的延长线上,y=![]() ,自变量取值范围为x>1.
,自变量取值范围为x>1.
详解:(1)∵AB∥DF,
∴![]() ,
,
∵BE=2CE,AB=3,
∴![]() ,
,
∴CF=![]() ;
;
(2)①若点E在线段BC上,如图1,设直线AB1与DC相交于点M.
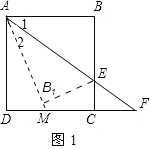
由题意翻折得:∠1=∠2.
∵AB∥DF,
∴∠1=∠F,
∴∠2=∠F,
∴AM=MF.
设DM=x,则CM=3-x.
又∵CF=1.5,
∴AM=MF=![]() -x,
-x,
在Rt△ADM中,AD2+DM2=AM2,
∴32+x2=(![]() -x)2,
-x)2,
∴x=![]() ,
,
∴DM=![]() ,AM=
,AM=![]() ,
,
∴sin∠DAB1=![]() ;
;
②若点E在边BC的延长线上,如图2,设直线AB1与CD延长线相交于点N.

同理可得:AN=NF.
∵BE=2CE,
∴BC=CE=AD.
∵AD∥BE,
∴![]() ,
,
∴DF=FC=![]() ,
,
设DN=x,则AN=NF=x+![]() .
.
在Rt△ADN中,AD2+DN2=AN2,
∴32+x2=(x+![]() )2,
)2,
∴x=![]() .
.
∴DN=![]() ,AN=
,AN=![]() ,sin∠DAB1=
,sin∠DAB1=![]() ;
;
(3)y=![]() ,自变量取值范围为x>0;若点E在边BC的延长线上,y=
,自变量取值范围为x>0;若点E在边BC的延长线上,y=![]() ,自变量取值范围为x>1.
,自变量取值范围为x>1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y关于x的二次函数y=ax2﹣bx+2(a≠0).
(1)当a=﹣2,b=﹣4时,求该函数图象的对称轴及顶点坐标.
(2)在(1)的条件下,Q(m,t)为该函数图象上的一点,若Q关于原点的对称点P也落在该函数图象上,求m的值.
(3)当该函数图象经过点(1,0)时,若A(
 ,y1),B(
,y1),B(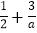 ,y2)是该函数图象上的两点,试比较y1与y2的大小.
,y2)是该函数图象上的两点,试比较y1与y2的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF.连结DE,过点E作EG⊥DE,使EG=DE,连结FG、FC
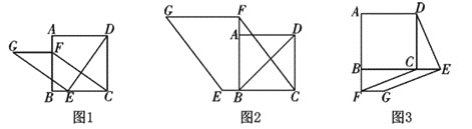
(1)请判断:FG与CE的数量关系是 ________,位置关系是________。
(2)如图2,若点E、F分别是边CB、BA延长线上的点,其他条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E、F分别是边BC、AB延长线上的点,其他条件不变,(1)中结论是否仍然成立?请直接写出你的判断。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的四个顶点分别在反比例函数
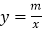 与
与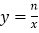 (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以点O为端点按顺时针方向依次作射线OA、OB、OC、OD.
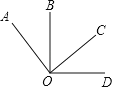
(1)若∠AOC、∠BOD都是直角,∠BOC=60°,求∠AOB和∠DOC的度数.
(2)若∠BOD=100°,∠AOC=110°,且∠AOD=∠BOC+70°,求∠COD的度数.
(3)若∠AOC=∠BOD=α,当α为多少度时,∠AOD和∠BOC互余?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学学生步行到郊外旅行,七年级
 班学生组成前队,步行速度为4千米
班学生组成前队,步行速度为4千米 小时,七
小时,七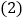 班的学生组成后队,速度为6千米
班的学生组成后队,速度为6千米 小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米
小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米 小时.
小时. 后队追上前队需要多长时间?
后队追上前队需要多长时间? 后队追上前队的时间内,联络员走的路程是多少?
后队追上前队的时间内,联络员走的路程是多少? 七年级
七年级 班出发多少小时后两队相距2千米?
班出发多少小时后两队相距2千米?
相关试题

