【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“南山”的概率.
参考答案:
【答案】(1) P=![]() ;(2) P=
;(2) P=![]()
【解析】分析:(1)由一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球,除汉字不同之外,小球没有任何区别,直接利用概率公式求解即可求得答案;
(2)首先根据题意列举出所有可能的结果与取出的两个球上的汉字恰能组成“美丽”或“南山”的情况,再利用概率公式即可求得答案.
本题解析:
(1)∵有汉字“美”、“丽”、“南”、“山”的四个小球,任取一球,共有4种不同结果,
∴球上汉字是“美”的概率为P=![]() ;
;
(2)列举如下:
美丽南山
美(丽,美)(南,美)(山,美);
丽(美,丽)(南,丽)(山,丽);
南(美,南)(丽,南)(山,南);
山(美,山)(丽,山)(南,山);
所有等可能的情况有12种,其中取出的两个球上的汉字恰能组成“美丽”或“南山”的情况有4种,
则P=![]() .
.
点睛: 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.注意掌握放回试验与不放回实验的区别.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式5x2﹣2x3+3x﹣1按x的降幂排列 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,联结BE、DF,DF交对角线于点P,且DE=DP.
(1)求证:AE=CP;
(2)求证:BE∥DF.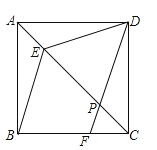
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:b是最大的负整数,且a,b,c满足|a+b|+(4-c)2016 =0,试回答问题:
(1)请直接写出a,b,c的值;
(2)若a,b,c所对应的点分别为A,B,C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0≤x≤1),请化简式子:|x+1|-|1-x|+2|x-4|;
(3)在(1)、(2)的条件下,点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和C分别以每秒3个单位长度和8个单位长度的速度向右运动,假设t秒后,若点B与点C之间的距离表示为BC,点A与B之间的距离表示为AB.请问:AB-BC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是两个可以自由转动的转盘,转盘A被分成三个面积相等的扇形,转盘B被分成两个面积相等的扇形.

(1)转动转盘A一次,所得到的数字是负数的概率为_______________
(2)转动两个转盘各一次,请用列表法或画树状图法求所得到的数字均是负数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,直线a∥b∥c∥d,且a与b,c与d之间的距离均为1,b与c之间的距离为2,现将正方形ABCD如图放置,使其四个顶点分别在四条直线上,求正方形的边长;
(2)在(1)的条件下,探究:将正方形ABCD改为菱形ABCD,如图2,当∠DCB=120°时,求菱形的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据4、4、4、5、5、6、7的众数和中位数分别是( )
A.4和4B.4和5C.7和5D.7和6
相关试题

