【题目】已知:b是最大的负整数,且a,b,c满足|a+b|+(4-c)2016 =0,试回答问题:
(1)请直接写出a,b,c的值;
(2)若a,b,c所对应的点分别为A,B,C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0≤x≤1),请化简式子:|x+1|-|1-x|+2|x-4|;
(3)在(1)、(2)的条件下,点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和C分别以每秒3个单位长度和8个单位长度的速度向右运动,假设t秒后,若点B与点C之间的距离表示为BC,点A与B之间的距离表示为AB.请问:AB-BC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
参考答案:
【答案】(1) a=-1,b=1,c=4;(2)8;(3) AB-BC的值是否随着时间t的变化而改变.
【解析】分析:(1)根据b是最大的负整数,即可得出b的值,再根据绝对值及偶次方的非负性即可得出a、c的值;(2)分析当0≤x≤1时,x+1、1-x、x-4的正负,去掉绝对值符号即可得出结论;(3)找出运动时间为t时,点A、B、C对应的数,再根据两点间的距离公式找出AB、BC的长度,二者做差后即可得出结论.
本题解析:
(1)∵b是最大的负整数,|a+b|+![]() =0,
=0,
∴b=1,a=b=1,c=4,
(2)∵0x1,
∴x+1>0,1x0,x4<0,
∴|x+1||1x|+2|x4|=x+1(1x)+2(4x)=8.
(3)ABBC的值随着时间t的变化而改变,理由如下:
运动时间为t时,点A对应的数为12t,点B对应的数为3t1,点C对应的数为8t+4,
∴AB=|12t(3t1)|=|5t2|,BC=|8t+4(3t1)|=|5t+5|,
∴ABBC=|5t2||5t5|.
当0t<![]() 时,ABBC=25t(55t)=3;
时,ABBC=25t(55t)=3;
当![]() t<1时,ABBC=5t2(55t)=10t7;
t<1时,ABBC=5t2(55t)=10t7;
当1t时,ABBC=5t2(5t5)=3.
综上所述:ABBC的值随着时间t的变化而改变。
点睛: 本题考查了有理数、绝对值和偶次方的非负性以及数轴,根据点的运动规则找出t秒后点对应的数是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进A,B两种钢笔,若购进A种钢笔2支,B种钢笔3支,共需90元;购进A种钢笔3支,B种钢笔5支,共需145元.
(1)求A、B两种钢笔每支各多少元?
(2)若该文具店要购进A,B两种钢笔共90支,总费用不超过1588元,并且A种钢笔的数量少于B种钢笔的数量,那么该文具店有哪几种购买方案?
(3)文具店以每支30元的价格销售B种钢笔,很快销售一空,于是,文具店决定在进价不变的基础上再购进一批B种钢笔,涨价卖出,经统计,B种钢笔售价为30元时,每月可卖68支;每涨价1元,每月将少卖4支,设文具店将新购进的B种钢笔每支涨价a元(a为正整数),销售这批钢笔每月获利W元,试求W与a之间的函数关系式,并且求出B种铅笔销售单价定为多少元时,每月获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式5x2﹣2x3+3x﹣1按x的降幂排列 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,联结BE、DF,DF交对角线于点P,且DE=DP.
(1)求证:AE=CP;
(2)求证:BE∥DF.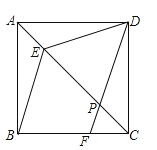
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“南山”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是两个可以自由转动的转盘,转盘A被分成三个面积相等的扇形,转盘B被分成两个面积相等的扇形.

(1)转动转盘A一次,所得到的数字是负数的概率为_______________
(2)转动两个转盘各一次,请用列表法或画树状图法求所得到的数字均是负数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,直线a∥b∥c∥d,且a与b,c与d之间的距离均为1,b与c之间的距离为2,现将正方形ABCD如图放置,使其四个顶点分别在四条直线上,求正方形的边长;
(2)在(1)的条件下,探究:将正方形ABCD改为菱形ABCD,如图2,当∠DCB=120°时,求菱形的边长.
相关试题

