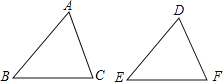
【题目】根据下列条件,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠DB.∠A=∠D,∠C=∠F,AC=EF
C.∠B=∠E,∠A=∠D,AC=EFD.AB=DE,BC=EF,∠B=∠E
参考答案:
【答案】D
【解析】
全等三角形的判定方法有:SAS,ASA,AAS,SSS,HL,而SSA,AAA都不能判定两三角形全等,根据以上内容判断即可.
解:A、根据AB=DE,BC=EF,∠A=∠D,SSA不能判定△ABC≌△DEF,故本选项错误;
B、根据∠A=∠D,∠C=∠F,AC=EF,而AC和EF不是对应边,不能判定△ABC≌△DEF,故本选项错误;
C、根据∠B=∠E,∠A=∠D,AC=EF,而AC与EF不是对应边,不能判定△ABC≌△DEF,故本选项错误;
D、根据AB=DE,BC=EF,∠B=∠E,根据SAS可以判定△ABC≌△DEF,故本选项正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△CEF的顶点C、E、F分别与正方形ABCD的顶点C、A、B重合.

(1)若正方形的边长为
 ,用含
,用含 的代数式表示:正方形ABCD的周长等于 ,△CEF的面积等于 .
的代数式表示:正方形ABCD的周长等于 ,△CEF的面积等于 .(2)如图2,将△CEF绕点A顺时针旋转,边CE和正方形的边AD交于点P. 连结AE, 设旋转角∠BCF=β.
①试证:∠ACF=∠DCE;
②若△AEP有一个内角等于60°,求β的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用一条直线分割一个三角形,如果能分割出等腰三角形,那么就称这条直线为该三角形的一条等腰分割线.在直角三角形ABC中,∠C=90°,AC=8,BC=6.

(1)如图(1),若 O 为 AB 的中点,则直线 OC_____△ABC 的等腰分割线(填“是”或“不是”)
(2)如图(2)已知△ABC 的一条等腰分割线 BP 交边 AC 于点 P,且 PB=PA,请求出 CP 的长度.
(3)如图(3),在△ABC 中,点 Q 是边 AB 上的一点,如果直线 CQ 是△ABC 的等腰分割线,求线段BQ 的长度等于 ______.(直接写出答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
点A、B在数轴上分别表示实数
 ,A、B两点这间的距离表示为
,A、B两点这间的距离表示为 ,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,
,当A、B两点中有一点在原点时,不妨设点A在原点,如图1, ;
; 
当A、B两点都不在原点时:
①如图2,点A、B都在原点的右边
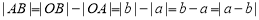 ;
;②如图3,点A、B都在原点的左边
 ;
;③如图4,点A、B在原点的两边
 .
.综上,数轴上A、B两点之间的距离
 .
.回答下列问题:
(1)数轴上表示2和5两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 ;
(2)数轴上表示
 和-1的两点A和B之间的距离是 ,如果
和-1的两点A和B之间的距离是 ,如果 ,那么
,那么 为 ;
为 ;(3)求
 的最小值.(提示:
的最小值.(提示: )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
 上的图象经过点
上的图象经过点 ,直线
,直线 与双曲线
与双曲线 在第二、四象限分别相交于P、Q两点,与x轴、y轴分别相交于C,D两点
在第二、四象限分别相交于P、Q两点,与x轴、y轴分别相交于C,D两点 求k的值;
求k的值; 连接OQ,是否存在实数b,使得
连接OQ,是否存在实数b,使得 ?若存在,请求出b的值;若不存在,请说明理由.
?若存在,请求出b的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】第十一届中国
 郑州
郑州 国际园林博览会于2017年9月29日在郑州航空港经济综合实验区开幕,共有园博园、双湖中央公园、苑陵故城遗址公园三个园区,“三园”作为我市新的热门旅游胜地,吸引了众多游客的目光,郑州市某中学一班、二班的老师计划组织本班学生于2017年11月18日前往参观游览,按照园区规定教师需购买普通票,学生购买学生票,两个班前往参观的教师人数、学生人数、计划购票总花费分别见如表:
国际园林博览会于2017年9月29日在郑州航空港经济综合实验区开幕,共有园博园、双湖中央公园、苑陵故城遗址公园三个园区,“三园”作为我市新的热门旅游胜地,吸引了众多游客的目光,郑州市某中学一班、二班的老师计划组织本班学生于2017年11月18日前往参观游览,按照园区规定教师需购买普通票,学生购买学生票,两个班前往参观的教师人数、学生人数、计划购票总花费分别见如表:班级
教师人数
 人
人
学生人数
 人
人
总的购票费用
 元
元
一班
4
40
1840
二班
5
45
2100
 每张普通票、学生票的票价分别为多少元?
每张普通票、学生票的票价分别为多少元? 为了节约费用,85名学生准备通过旅行社购买团体票,每张30元,9名教师准备参加2017年11月16日由郑州市总工会推出了“10元畅游园博园”的活动,本次活动将为郑州市工会会员送上2000张园博园的门票,并于11月16日16:00、20:00两个整点在微信平台进行电子抢票
为了节约费用,85名学生准备通过旅行社购买团体票,每张30元,9名教师准备参加2017年11月16日由郑州市总工会推出了“10元畅游园博园”的活动,本次活动将为郑州市工会会员送上2000张园博园的门票,并于11月16日16:00、20:00两个整点在微信平台进行电子抢票 每人1张
每人1张 ,抢到电子票的工会会员就可以花费10元购买园博园门票,已知这两个班的9名教师都具有抢票资格
,抢到电子票的工会会员就可以花费10元购买园博园门票,已知这两个班的9名教师都具有抢票资格 若最终这9名教师、85名学生购买门票的总花费不能超过2900元,则至少需要几名教师抢到“10元票”?
若最终这9名教师、85名学生购买门票的总花费不能超过2900元,则至少需要几名教师抢到“10元票”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AB=10,AC=
 ,BC 边上的高 AD=6,则另一边 BC 等于( )
,BC 边上的高 AD=6,则另一边 BC 等于( )A.10B.8C.6 或 10D.8 或 10
相关试题

