【题目】已知点A,B在数轴上对应的数分别为a,b,且|a+4|+(b-2)2=0,点A,B之间的距离记作AB.
(1)线段AB的长为 ;(直接写出结果)
(2)若动点P在数轴上对应的数为x.
①当PA+PB的值最小时,则奇数x的值为 ;(直接写出结果)
②当PA+PB=14时,求x的值;
(3)当动点P在点A的左侧,M,N分别是PA,PB的中点,当点P在A的左侧移动时,聪明的小明同学在计算PM+PN和PN-PM的值时发现:其中只有一个的值是不变的,请你判断出哪一个的值不变,并求这个值.
参考答案:
【答案】(1)6(2)①-3,-1,1 ②x的值为-8或6(3)PN-PM=3
【解析】
(1)根据非负数的性质求出a、b的值即可解决问题;
(2)①当PA+PB的值最小时,表示数x的点P在线段AB上,由此即可解决问题;
②分两种情形列出方程求解即可;
(3)PN-PM的值不变.列出PN、PM的代数式即可解决问题;
解:(1)∵|a+4|+(b-2)2=0,
又∵|a+4|≥0,(b-2)2≥0,
∴a=-4,b=2,
∴AB=2-(-4)=6,
故答案为6.
(2)①当PA+PB的值最小时,则奇数x的值为-3,-1,1;
故答案为-3,-1,1;
②当点P在点A左边时,2-x+-4-x=14,解得x=-8;
当点P在点B右边时,x-2+x+4=14,解得x=6,
∴x的值为-8或6.
(3)结论:PN-PM的值不变.
理由:∵PN=![]() (2-x),PM=
(2-x),PM=![]() (-4-x),
(-4-x),
∴PN-PM=1-![]() x+2+
x+2+![]() x=3.
x=3.
∴PN-PM的值不变,这个值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=k1x+2与反比例函数
 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
(1)k1= , k2=;
(2)根据函数图象可知,当y1>y2时,x的取值范围是;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 为
为 的角平分线上的一点,点
的角平分线上的一点,点 在边
在边 上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边
上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边 上取一点
上取一点 ,使得
,使得 ,这时他发现
,这时他发现 与
与 之间有一定的数量关系,请你写出
之间有一定的数量关系,请你写出 与
与 的数量关系__________.
的数量关系__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红红有5张写着以下数字的卡片,请你按要求抽出卡片,完成下列各题:
+3 +2 +1 0 -2
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最小,最小值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1-(-2)]),请另写出两种符合要求的运算式子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出所有满足下列条件的数:
(1)大于-
 且小于
且小于 的所有整数;
的所有整数;(2)小于
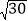 的所有正整数;
的所有正整数;(3)绝对值小于
 的所有整数.
的所有整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD相交于O,EF经过点O,分别交AD,BC于E,F,已知ABCD的面积是
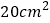 ,则图中阴影部分的面积是
,则图中阴影部分的面积是

A. 12
 B. 10
B. 10 C.
C.  D.
D. 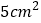
相关试题

