【题目】如图,已知点![]() 为
为![]() 的角平分线上的一点,点
的角平分线上的一点,点![]() 在边
在边![]() 上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边
上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边![]() 上取一点
上取一点![]() ,使得
,使得![]() ,这时他发现
,这时他发现![]() 与
与![]() 之间有一定的数量关系,请你写出
之间有一定的数量关系,请你写出![]() 与
与![]() 的数量关系__________.
的数量关系__________.

参考答案:
【答案】![]() 或
或![]()
【解析】
如图,以O为圆心,以OD为半径作弧,交OB于E2,连接PE2,根据SAS证△E2OP≌△DOP,推出E2P=PD,得出此时点E2符合条件,此时∠OE2P=∠ODP;以P为圆心,以PD为半径作弧,交OB于另一点E1,连接PE1,根据等腰三角形性质推出∠PE2E1=∠PE1E2,求出∠OE1P+∠ODP=180°即可.
(1)如图,以O为圆心,以OD为半径作弧,交OB于E2,连接PE2,

∵OP是∠AOB的平分线,
∴∠E2OP=∠DOP,
在△EOP和△DOP中

∴△E2OP≌△DOP(SAS),
∴∠OE2P=∠ODP,PE2=PD;
(2)以P为圆心,以PD为半径作弧,交OB于另一点E1,连接PE1,
∵PE1=PE2,
∴∠PE2E1=∠PE1E2,
∴由邻补角定义可得:∠PE1O+∠PE1E2=180![]() ,
,
∴∠PE1O+∠PDO=180![]() .
.
综合上述:![]() 或
或![]()
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,动点P在∠ABC的平分线BD上,动点M在BC边上,若BC=3,∠ABC=45°,则PM+PC的最小值是( )

A. 2 B.
 C.
C.  D. 3
D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=k1x+2与反比例函数
 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
(1)k1= , k2=;
(2)根据函数图象可知,当y1>y2时,x的取值范围是;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B在数轴上对应的数分别为a,b,且|a+4|+(b-2)2=0,点A,B之间的距离记作AB.
(1)线段AB的长为 ;(直接写出结果)
(2)若动点P在数轴上对应的数为x.
①当PA+PB的值最小时,则奇数x的值为 ;(直接写出结果)
②当PA+PB=14时,求x的值;
(3)当动点P在点A的左侧,M,N分别是PA,PB的中点,当点P在A的左侧移动时,聪明的小明同学在计算PM+PN和PN-PM的值时发现:其中只有一个的值是不变的,请你判断出哪一个的值不变,并求这个值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红红有5张写着以下数字的卡片,请你按要求抽出卡片,完成下列各题:
+3 +2 +1 0 -2
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最小,最小值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1-(-2)]),请另写出两种符合要求的运算式子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出所有满足下列条件的数:
(1)大于-
 且小于
且小于 的所有整数;
的所有整数;(2)小于
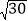 的所有正整数;
的所有正整数;(3)绝对值小于
 的所有整数.
的所有整数.
相关试题

