【题目】已知抛物线y=ax2+bx+c的顶点为A,经过点B(0,3)和点(2,3),与x轴交于C,D两点,(点C在点D的左侧),且OD=OB.
(1)求这条抛物线的表达式;
(2)连接AB,BD,DA,试判断△ABD的形状;
(3)点P是BD上方抛物线上的动点,当P运动到什么位置时,△BPD的面积最大?求出此时点P的坐标及△BPD的面积.
参考答案:
【答案】
(1)
解:∵B(0,3)和点(2,3)的纵坐标相同,
∴抛物线的对称轴为x=1,OB=3.
∵OD=OB,
∴OD=3.
∵抛物线与x轴交于C,D两点,(点C在点D的左侧),
∴D(3,0).
将点B(0,3)、(2,3)、(3,0)代入抛物线的解析式得:  ,
,
解得:a=﹣1,b=2,c=3.
∴抛物线的解析式为y=﹣x2+2x+3
(2)
解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴点A的坐标为(1,4).
依据两点间的距离公式可知:AB2=(1﹣0)2+(4﹣3)2=2,AD2=(3﹣1)2+(4﹣0)2=20,BD2=(3﹣0)2+(0﹣3)2=18,
∴AB2+BD2=AD2.
∴△ABD为直角三角形
(3)
解:如图所示:连结OP.

设点P的坐标为(x,﹣x2+2x+3).
△DBP的面积=△OBP的面积+△ODP的面积﹣△BOD的面积
= ![]() ×3×x+
×3×x+ ![]() ×3×(﹣x2+2x+3)﹣
×3×(﹣x2+2x+3)﹣ ![]() ×3×3
×3×3
=﹣ ![]() x2+
x2+ ![]() x
x
=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() .
.
∴当x= ![]() 时,△DBP的面积最大,最大值为
时,△DBP的面积最大,最大值为 ![]() .
.
将x= ![]() 代入抛物线的解析式得y=
代入抛物线的解析式得y= ![]() ,
,
∴点P的坐标为( ![]() ,
, ![]() )
)
【解析】(1)由点B的坐标可知OB=3,OD=3,故此可得到点D的坐标,然后利用待定系数法求解即可;(2)先由抛物线的解析式求得点A的坐标,然后利用两点间的距离公式可求得AB、AD、BD的长,最后利用勾股定理的逆定理进行判断即可(3)如图所示:连结OP.设点P的坐标为(x,﹣x2+2x+3).依据△DBP的面积=△OBP的面积+△ODP的面积﹣△BOD的面积,列出△DBP的面积与x的函数关系式,然后依据二次函数的性质求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为60°,已知坡角为30°,你能求出楼房AB的高度吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况.小强在全校范围内随机抽取了若干名学生并就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图.

回答下列问题:
(1)这次被抽查的学生共有人,扇形统计图中,“B组”所对应的圆心角的度数为;
(2)补全条形统计图;
(3)已知该中学共有学生2500人,请估计这日午饭有剩饭的学生人数;若按平均每人剩10克米饭计算,这日午饭将浪费多少千克米饭? -
科目: 来源: 题型:
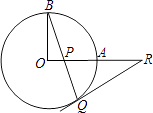
查看答案和解析>>【题目】如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点,BP的延长线交⊙O于Q,过Q的⊙O的切线交OA的延长线于R.求证:RP=RQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.

(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F= ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列几何体中主视图、左视图、府视图都相同的是( )

A.半球
B.圆柱
C.球
D.六棱柱 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点.
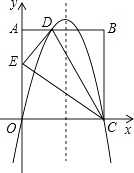
(1)求抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使四边形MENC是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
相关试题

