【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF= ![]() BC,连接CD和EF.
BC,连接CD和EF. 
(1)求证:四边形DCFE是平行四边形;
(2)求EF的长.
参考答案:
【答案】
(1)证明:∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE= ![]() BC
BC
∵延长BC至点F,使CF= ![]() BC,
BC,
∴DE=FC;
(2)解:∵DE∥FC,DE=FC
∴四边形DEFC是平行四边形,
∴DC=EF,
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴DC=EF= ![]() =
= ![]() .
.
【解析】(1)直接利用三角形中位线定理得出DE∥BC,DE= ![]() BC,进而得出DE=FC;(2)利用平行四边形的判定与性质得出DC=EF,进而利用等边三角形的性质以及勾股定理得出EF的长.
BC,进而得出DE=FC;(2)利用平行四边形的判定与性质得出DC=EF,进而利用等边三角形的性质以及勾股定理得出EF的长.
【考点精析】掌握等边三角形的性质和三角形中位线定理是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形有一个角为100°,顶角等于________ 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,对称轴为直线x=
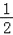 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的有( ).
①相等的圆心角所对的弧相等;
②平分弦的直径也平分弦所对的弧;
③长度相等的两条弧是等弧;
④经过圆心的每一条直线将圆分成两条等弧.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,y甲、y乙与x之间的函数图象如图所示.

(1)甲的速度是km/h;
(2)当1≤x≤5时,求y乙关于x的函数解析式;
(3)当乙与A地相距240km时,甲与A地相距km. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数的个位上的数字是1,十位上的数字比个位上的数字大a,则这个两位数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天最高气温是2℃,最低气温是-11℃,则这天最高气温与最低气温的差是( )
A.-9℃B.9℃C.13℃D.-13℃
相关试题

