【题目】如图,![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径画弧,分别交
长为半径画弧,分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() ,则除
,则除![]() 外,图中是等腰三角形的还有( )
外,图中是等腰三角形的还有( )
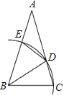
A.1个B.2个C.3个D.4个
参考答案:
【答案】D
【解析】
等腰三角形还有△BDC,△BED,△BAD,△AED,根据半径相等得出△BDC和△BED是等腰三角形,根据等腰三角形性质和三角形的内角和定理即可推出其它三角形也是等腰三角形.
解:除△ABC外,等腰三角形还有△BDC,△BED,△BAD,△AED,
理由是:∵BD=BC=BE,
∴△BDC和△BED是等腰三角形,
∵∠A=36°,AC=AB,
∴∠C=∠ABC=![]() (180°∠A)=72°,
(180°∠A)=72°,
∵BD=BC,
∴∠BDC=∠C=72°,
∴∠CBD=180°72°72°=36°,
∴∠ABD=72°36°=36°=∠A,
∴BD=AD,即△ABD是等腰三角形,
∵∠ABD=36°,BE=BD,
∴∠BDE=∠BED=![]() (180°∠ABD)=72°,
(180°∠ABD)=72°,
∵∠ADE=180°72°72°=36°=∠A,
∴AE=DE,
∴△AED是等腰三角形,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
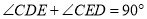 ,EM平分
,EM平分 ,并与CD边交于点M.DN平分
,并与CD边交于点M.DN平分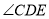 ,
,并与EM交于点N.
(1)依题意补全图形,并猜想
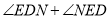 的度数等于 ;
的度数等于 ;(2)证明以上结论.
证明:∵ DN平分
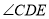 ,EM平分
,EM平分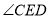 ,
, ∴
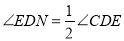 ,
,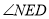 = .
= .(理由: )
∵
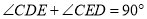 ,
,∴
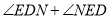 = ×(∠ +∠ )= ×90°= °.
= ×(∠ +∠ )= ×90°= °.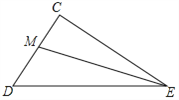
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图
 ,试判断
,试判断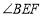 、
、 、
、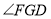 之间的关系.并说明理由.
之间的关系.并说明理由.(2)如图
 ,
,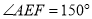 ,
,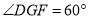 .试判断
.试判断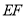 和
和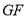 的位置关系,并说明理由.
的位置关系,并说明理由.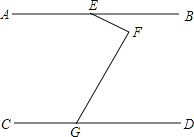
-
科目: 来源: 题型:
查看答案和解析>>【题目】用方程解答下列问题.
(1)一个角的余角比它的补角的
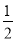 还少15°,求这个角的度数;
还少15°,求这个角的度数;(2)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问共有多少人?这个物品的价格是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】

A.12 B. 24 C. 12
 D. 16
D. 16
-
科目: 来源: 题型:
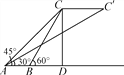
查看答案和解析>>【题目】如图,两个观察者从A,B两地观测空中C处一个气球,分别测得仰角为45°和60°.已知A,B两地相距100 m.当气球沿与AB平行的路线飘移20 s后到达点C′,在A处测得气球的仰角为30°.求:
(1)气球飘移的平均速度(精确到0.1 m/s);
(2)在B处观测点C′的仰角(精确到度).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60 m到达点C,测得点B在点C的北偏东60°方向,如图②.
(1)求∠CBA的度数;
(2)求出这段河的宽(结果精确到1 m,参考数据:
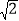 ≈1.41,
≈1.41,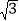 ≈1.73).
≈1.73).
① ②
相关试题

