【题目】已知![]() 、
、![]() 在直线
在直线![]() 上,
上,![]() ,点
,点![]() 线段
线段![]() 的中点,点
的中点,点![]() 是直线
是直线![]() 上的一个动点.
上的一个动点.
(1)若![]() ,求
,求![]() 的长;
的长;
(2)若![]() 是线段
是线段![]() 的中点,
的中点,![]() 是
是![]() 的中点,求
的中点,求![]() 的长.
的长.
参考答案:
【答案】(1)![]() 的长为:9或19;(2)MN=14
的长为:9或19;(2)MN=14
【解析】
(1) 分当P在CB上时、当P在CB的延长线上时两种情况进行分类讨论即可;
(2)分当P在AB线上时、当P在AB的延长线上时、当P在BA的延长线上时三种情况进行讨论,利用中点的性质将MM的和差分别表示出来即可得出答案.
解:(1)∵点![]() 线段
线段![]() 的中点,
的中点,![]() ,
,
∴![]()
当P在CB上时,如图:
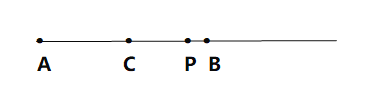
∵![]()
∴CP=BC-CP=14-5=9
当P在CB的延长线上时,如图:
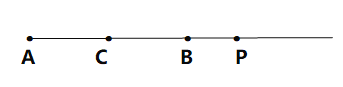
∵![]()
∴CP=BC+BP=14+5=19
∴![]() 的长为:9或19
的长为:9或19
(2)∵M为AP的中点
∴![]()
∵N为BP的中点
∴![]()
当P在AB线上时,如图

![]()
当P在AB的延长线上时,如图

![]()
当P在BA的延长线上时,如图

![]()
综上所述:MM=14
-
科目: 来源: 题型:
查看答案和解析>>【题目】一水果店主分两批购进某一种水果,第一批所用资金为2400元,因天气原因,水果涨价,第二批所用资金是2700元,但由于第二批单价比第一批单价每箱多10元,以致购买的数量比第一批少25%.
(1)该水果店主购进第一批这种水果的单价是多少元?
(2)该水果店主计两批水果的售价均定为每箱40元,实际销售时按计划无损耗售完第一批后,发现第二批水果品质不如第一批,于是该店主将售价下降a%销售,结果还是出现了20%的损耗,但这两批水果销售完后仍赚了不低于1716元,求a的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为打造引江枢纽风光带,一段长为1.2千米的河道整治任务交由甲、乙两个工程队接力完成,共用时60天. 已知甲队每天整治24米,乙队每天整治16米.
(1)根据题意,小明、小丽分别列出如下的一元一次方程(尚不完整): 小明:
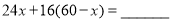 . 小丽:
. 小丽: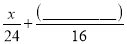 =60. 请分别指出上述方程中
=60. 请分别指出上述方程中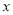 的意义,并补全方程: 小明:
的意义,并补全方程: 小明: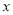 表示 . 小丽:
表示 . 小丽: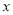 表示 .
表示 .(2)请选择其中一种方法,求甲、乙两队分别整治河道多少米?(写出完整的解答过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.
(1)若正方形ABCD边长为3,DF=4,求CG的长;
(2)求证:EF+EG=
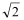 CE.
CE.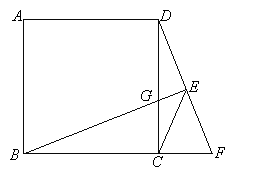
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若
 ,则称
,则称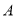 与
与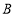 是关于
是关于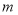 的关联数.例如:若
的关联数.例如:若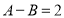 ,则称
,则称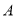 与
与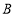 是关于2的关联数;
是关于2的关联数;(1)若3与
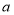 是关于2的关联数,则
是关于2的关联数,则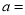 _______.
_______.(2)若
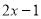 与
与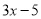 是关于2的关联数,求
是关于2的关联数,求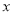 的值.
的值.(3)若
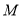 与
与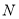 是关于
是关于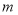 的关联数,
的关联数, 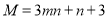 ,
,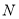 的值与
的值与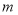 无关,求
无关,求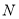 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
关于x的方程:
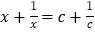 的解是
的解是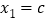 ,
,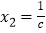 ;
; 即
即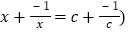 的解是
的解是 ;
;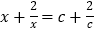 的解是
的解是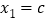 ,
,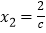 ;
;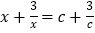 的解是
的解是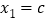 ,
,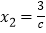 ;
;
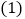 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程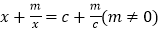 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.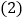 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:
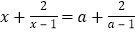 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2020年8月连淮扬镇铁路正式通车,高邮迈入高铁时代,动车的平均速度为
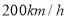 (动车的长度不计),高铁的平均速度为
(动车的长度不计),高铁的平均速度为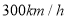 (高铁的长度不计),扬州市内依次设有6个站点,宝应站、高邮北站、高邮高铁站、邵伯站、江都站、扬州高铁站,假设每两个相邻站点之间的路程都相等,已知一列动车、一列高铁同时经过宝应站开往扬州高铁站,若中途不停靠任何站点,到达扬州高铁站时高铁比动车将早到10分钟
(高铁的长度不计),扬州市内依次设有6个站点,宝应站、高邮北站、高邮高铁站、邵伯站、江都站、扬州高铁站,假设每两个相邻站点之间的路程都相等,已知一列动车、一列高铁同时经过宝应站开往扬州高铁站,若中途不停靠任何站点,到达扬州高铁站时高铁比动车将早到10分钟(1)求宝应站到扬州高铁站的路程;
(2)若一列动车6:00从宝应站出发,每个站点都停靠4分钟,一列高铁6:18从宝应站出发,只停靠高邮北站、江都站,每个站点都停靠4分钟.
①求高铁经过多长时间追上动车;
②求高铁经过多长时间后,与动车的距离相距20千米.
相关试题

