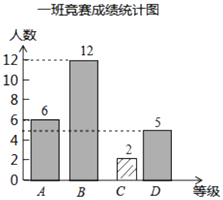
【题目】罗山县尚文学校组织了一次环保知识竞赛，每班选25名同学参加比赛，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为100分、90分、80分、79分，学校将某年级的一班和二班的成绩整理并绘制成如下的统计图：请根据以上提供的信息解答下列问题：
（1）把一班竞赛成绩统计图补充完整：
（2）填表：

平均数（分）

中位数（分）

众数（分）

一班

90

二班

87.6

80


（3）请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析；①从平均数和中位数方面来比较一班和二班的成绩；②从平均数和众数方面来比较一班和二班的成绩；③从B级以上（包括B级）的人数方面来比较一班和二班的成绩．

参考答案：

【答案】
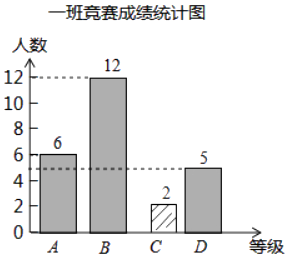
（1）解：如图所示：


（2）87.6；90；100
（3）解：①从平均数和中位数的角度来比较一班的成绩更好；

②从平均数和众数的角度来比较二班的成绩更好；

③从B级以上（包括B级）的人数的角度来比较一班的成绩更好.


【解析】（1）一班中C级的有25﹣6﹣12﹣5=2人，

如图所示：（2）一班的平均数为：a=（6×100+12×90+2×80+70×5）÷25=87.6；

一班的中位数为：b=90；

一班的众数为：c=100；（3）

所以答案是：（2）87.6；90；100

【考点精析】解答此题的关键在于理解中位数、众数的相关知识，掌握中位数是唯一的，仅与数据的排列位置有关，它不能充分利用所有数据；众数可能一个，也可能多个，它一定是这组数据中的数．

关闭