【题目】周末,甲从家出发前往与家相距![]() 千米的旅游景点旅游,以
千米的旅游景点旅游,以![]() 千米/时的速度步行
千米/时的速度步行![]() 小时后,改骑自行车以
小时后,改骑自行车以![]() 千米/时的速度继续向目的地出发,乙在甲前面
千米/时的速度继续向目的地出发,乙在甲前面![]() 千米处,在甲出发
千米处,在甲出发![]() 小时后开车追赶甲,两人同时到达目的地.设甲、乙两人离甲家的距离
小时后开车追赶甲,两人同时到达目的地.设甲、乙两人离甲家的距离![]() (千米)与甲出发的时间
(千米)与甲出发的时间![]() (小时)之间的函数关系如图所示.
(小时)之间的函数关系如图所示.
(1)求乙的速度;
(2)求甲出发多长时间后两人第一次相遇;
(3)求甲出发几小时后两人相距![]() 千米. .
千米. .

参考答案:
【答案】(1)乙的速度为![]() 千米/时;(2)甲出发
千米/时;(2)甲出发![]() 小时后两人第一次相遇;(3)甲出发
小时后两人第一次相遇;(3)甲出发![]() 小时或
小时或![]() 小时或
小时或![]() 小时后两人相距
小时后两人相距![]() 千米
千米
【解析】
(1)先求出甲走完全程的时间就可求出乙走完全程的时间,由速度等于路程除以时间即可解题,(2)设直线AB的解析式为y=kx+b,利用待定系数法即可解题,(3)分类讨论即可
解: (1)甲行驶完全程的时间为:![]() 小时.
小时.
乙的速度为:![]() 千米/时.
千米/时.
答:乙的速度为![]() 千米/时;
千米/时;
(2)设直线![]() 的解析式为y=kx+b:由题意,得
的解析式为y=kx+b:由题意,得
![]()
解得: ![]()
![]()
当![]() 时,
时,
![]() ,得
,得![]() .
.
答:甲出发![]() 小时后两人第一次相遇;
小时后两人第一次相遇;
(3)当乙不动时,
当![]() 时,
时,
解得:![]() .
.
当![]() 时
时
解得:![]() .
.
当甲乙均在运动时,设运动的时间为![]() ,
,
则 ![]() (
(![]() 为乙的速度),
为乙的速度),
解得![]() .
.
答:甲出发![]() 小时或
小时或![]() 小时或
小时或![]() 小时后两人相距
小时后两人相距![]() 千米.
千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 的对角线
的对角线 经过的坐标原点,矩形的边分别平行于坐标轴,点
经过的坐标原点,矩形的边分别平行于坐标轴,点 在反比例函数
在反比例函数 的图象上,若点
的图象上,若点 的坐标为
的坐标为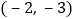 ,则
,则 的值为________.
的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.鞋子的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组
“鞋码”与鞋长换算的对应数值:[注:“鞋码”是表示鞋子大小的一种号码]
鞋长(cm)
16
19
21
24
鞋码(号)
22
28
32
38
(1)设鞋长为x,“鞋码”为y,试判断点(x,y)在你学过的哪种函数的图象上?
(2)求x、y之间的函数关系式;(3)如果某人穿44号“鞋码”的鞋,那么他的鞋长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道当电压一定时,电流与电阻成反比例函数关系.现有某学生利用一个最大电阻为
 的滑动变阻器及一电流表测电源电压,结果如图所示.
的滑动变阻器及一电流表测电源电压,结果如图所示.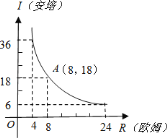
 电流
电流 (安培)与电阻
(安培)与电阻 (欧姆)之间的函数解析式为________;
(欧姆)之间的函数解析式为________; 当电阻在
当电阻在 之间时,电流应在________范围内,电流随电阻的增大而________;
之间时,电流应在________范围内,电流随电阻的增大而________; 若限制电流不超过
若限制电流不超过 安培,则电阻在________之间.
安培,则电阻在________之间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数( )

A. 24°B. 25°C. 30°D. 35°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,
 ,边
,边 、
、 都在
都在 轴的正半轴上,点
轴的正半轴上,点 的坐标为
的坐标为 ,
, ,
, .反比例函数
.反比例函数 的图象经过点
的图象经过点 ,交
,交 边于点
边于点 .则
.则 的值为________.
的值为________.
相关试题

