【题目】如图,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴相交于点
轴相交于点![]() ,顶点为
,顶点为![]() .
.

![]() 直接写出
直接写出![]() 、
、![]() 、
、![]() 三点的坐标和抛物线的对称轴.
三点的坐标和抛物线的对称轴.
![]() 连接
连接![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
参考答案:
【答案】![]() 顶点
顶点![]() 的坐标为
的坐标为![]() ,对称轴为直线
,对称轴为直线![]() ;
;![]() .
.
【解析】
(1)设x=0,则能够求出y轴交点C的坐标,设y=0,则能够求出和x轴交点A,B的坐标,再用配方法求出其顶点的坐标即可;
(2)由(1)可知AB的长,OC的长,利用三角形的面积公式即可求出△ABC的面积.
(1)设x=0,则y=3,所以出y轴交点C的坐标为(0,3);
设y=0,则y=﹣x2+2x+3=0,解得:x=3或﹣1.
∵点A在点B左侧,∴A(﹣1,0),B(3,0).
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4),对称轴为直线x=1;
(2)∵C(0,3),A(﹣1,0),B(3,0),∴AB=4,OC=3,∴S△ACB=![]() ×ABOC=
×ABOC=![]() ×4×3=6.
×4×3=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,抛物线
,抛物线 经过
经过 、
、 两点.
两点. 求抛物线的解析式;
求抛物线的解析式; 如图,点
如图,点 是直线
是直线 上方抛物线上的一动点,当
上方抛物线上的一动点,当 面积最大时,请求出点
面积最大时,请求出点 的坐标和
的坐标和 面积的最大值?
面积的最大值? 在
在 的结论下,过点
的结论下,过点 作
作 轴的平行线交直线
轴的平行线交直线 于点
于点 ,连接
,连接 ,点
,点 是抛物线对称轴上的动点,在抛物线上是否存在点
是抛物线对称轴上的动点,在抛物线上是否存在点 ,使得以
,使得以 、
、 、
、 、
、 为顶点的四边形是平行四边形?如果存在,请直接写出点
为顶点的四边形是平行四边形?如果存在,请直接写出点 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售某种玩具,进货价为
 元.根据市场调查:在一段时间内,销售单价是
元.根据市场调查:在一段时间内,销售单价是 元时,销售量是
元时,销售量是 件,而销售单价每上涨
件,而销售单价每上涨 元,就会少售出
元,就会少售出 件玩具,超市要完成不少于
件玩具,超市要完成不少于 件的销售任务,又要获得最大利润,则销售单价应定为________元.
件的销售任务,又要获得最大利润,则销售单价应定为________元. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数的图象经过点
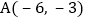 .
. 写出函数表达式;
写出函数表达式; 这个函数的图象在哪几个象限?
这个函数的图象在哪几个象限? 随
随 的增大怎样变化?
的增大怎样变化? 点
点 、
、 在这个函数的图象上吗?
在这个函数的图象上吗? 如果点
如果点 在图象上,求
在图象上,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 .
. 当抛物线的顶点在
当抛物线的顶点在 轴上时,求该抛物线的解析式;
轴上时,求该抛物线的解析式; 不论
不论 取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式; 若有两点
若有两点 ,且该抛物线与线段
,且该抛物线与线段 始终有交点,请直接写出
始终有交点,请直接写出 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D在边BC上,点E在边AC上,且AD=AE.
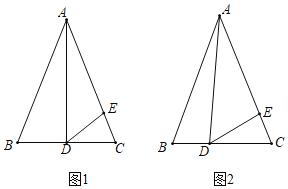
(1)如图1,当AD是边BC上的高,且∠BAD=30°时,求∠EDC的度数;
(2)如图2,当AD不是边BC上的高时,请判断∠BAD与∠EDC之间的关系,并加以证明.
-
科目: 来源: 题型:
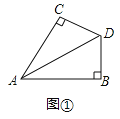
查看答案和解析>>【题目】如图,
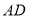 平分
平分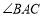 ,且
,且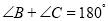 .
.(1)在图1中,当
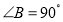 时,求证:
时,求证: ;
;
(2)在图2中,当
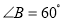 时,求证:
时,求证: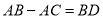 .
.
相关试题

