【题目】在△ABC中,AB=AC,点D在边BC上,点E在边AC上,且AD=AE.
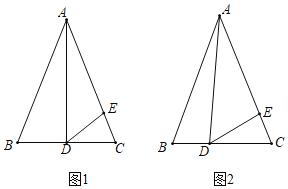
(1)如图1,当AD是边BC上的高,且∠BAD=30°时,求∠EDC的度数;
(2)如图2,当AD不是边BC上的高时,请判断∠BAD与∠EDC之间的关系,并加以证明.
参考答案:
【答案】(1)15°;(2)∠BAD=2∠EDC,证明详见解析.
【解析】
(1)由AD是边BC上的高,得到∠ADC=90°,根据等腰三角形的性质即可得到结论;
(2)根据等腰三角形的性质得到∠B=∠C,∠ADE=∠AED,根据三角形外角的性质得到∠ADC=∠B+∠BAD,∠AED=∠C+∠EDC,于是得到结论.
(1)∵AD是边BC上的高,
∴∠ADC=90°,
∵AB=AC,
∴AD是∠BAC的角平分线,
∴∠BAD=∠CAD,
∵∠BAD=30°,
∴∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°;
(2)∠BAD=2∠EDC,
理由:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∵∠ADC=∠B+∠BAD,∠AED=∠C+∠EDC,
∴∠B+∠BAD=∠ADC=∠ADE+∠EDC=∠AED+∠∠EDC=∠C+2∠EDC,
∴∠BAD=2∠EDC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数的图象经过点
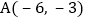 .
.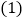 写出函数表达式;
写出函数表达式; 这个函数的图象在哪几个象限?
这个函数的图象在哪几个象限? 随
随 的增大怎样变化?
的增大怎样变化? 点
点 、
、 在这个函数的图象上吗?
在这个函数的图象上吗? 如果点
如果点 在图象上,求
在图象上,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
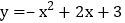 与
与 轴相交于点
轴相交于点 、
、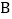 两点(点
两点(点 在点
在点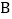 左侧),与
左侧),与 轴相交于点
轴相交于点 ,顶点为
,顶点为 .
.
 直接写出
直接写出 、
、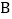 、
、 三点的坐标和抛物线的对称轴.
三点的坐标和抛物线的对称轴. 连接
连接 、
、 ,求
,求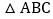 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
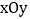 中,抛物线
中,抛物线 .
. 当抛物线的顶点在
当抛物线的顶点在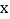 轴上时,求该抛物线的解析式;
轴上时,求该抛物线的解析式; 不论
不论 取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式; 若有两点
若有两点 ,且该抛物线与线段
,且该抛物线与线段 始终有交点,请直接写出
始终有交点,请直接写出 的取值范围.
的取值范围. -
科目: 来源: 题型:
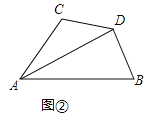
查看答案和解析>>【题目】如图,
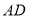 平分
平分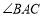 ,且
,且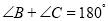 .
.(1)在图1中,当
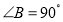 时,求证:
时,求证: ;
;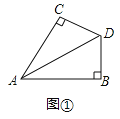
(2)在图2中,当
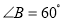 时,求证:
时,求证: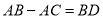 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 的坐标为
的坐标为 ,过点
,过点 作
作 轴的平行线交
轴的平行线交 轴于点
轴于点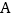 ,交双曲线
,交双曲线 于点
于点 ,作
,作 交双曲线
交双曲线 于点
于点 ,连接
,连接 、
、 ,已知
,已知 .
.
 求
求 的值.
的值. 求
求 的面积.
的面积. 试判断
试判断 与
与 是否相似,并说明理由.
是否相似,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(问题探究)
将三角形
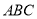 纸片沿
纸片沿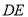 折叠,使点A落在点
折叠,使点A落在点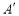 处.
处.(1)如图,当点A落在四边形
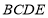 的边
的边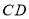 上时,直接写出
上时,直接写出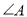 与
与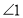 之间的数量关系;
之间的数量关系;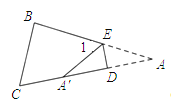
(2)如图,当点A落在四边形
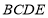 的内部时,求证:
的内部时,求证: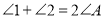 ;
;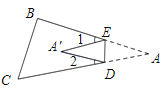
(3)如图,当点A落在四边形
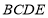 的外部时,探索
的外部时,探索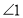 ,
,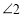 ,
,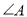 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;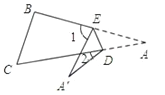
(拓展延伸)
(4)如图,若把四边形
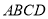 纸片沿
纸片沿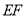 折叠,使点A、D落在四边形
折叠,使点A、D落在四边形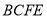 的内部点
的内部点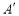 、
、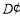 的位置,请你探索此时
的位置,请你探索此时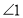 ,
,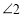 ,
,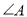 ,
,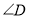 之间的数量关系,写出你发现的结论,并说明理由.
之间的数量关系,写出你发现的结论,并说明理由.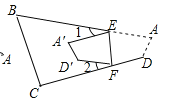
相关试题

