【题目】如图,四边形ABCD是平行四边形,点E、F在BC上,且CF=BE,连接DE,过点F作FG⊥AB于点G.

(1)如图1,若∠B=60°,DE平分∠ADC,且 ![]() ,
,![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.
(2)点H在GF上,且HE=HF,延长EH交AC,CD于点O,Q,连接AQ,若AC=BC=EQ,∠EQC=45°,求证:![]() .
.
参考答案:
【答案】(1)18![]() +9;(2)见详解.
+9;(2)见详解.
【解析】
(1)由角平分线的定义及平行四边形的性质,得CD=CE=6,从而得CF=![]() ,进而得BC=6+
,进而得BC=6+![]() .过点A作AM⊥BC于点M,得AM=
.过点A作AM⊥BC于点M,得AM= ![]() ,根据平行四边形的面积公式,即可求解.
,根据平行四边形的面积公式,即可求解.
(2)过点C作CN⊥EQ于点N,其延长线交AD于点K,先证△BGF≌△CNE(AAS),再证△ACK≌△QEC(ASA),进而即可得到结论.
(1)∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠CED,
∴∠CED=∠CDE,
∴CD=CE=6,
∵![]() ,
,
∴CF=![]() ,
,
∵CF=BE,
∴BE=![]() ,
,
∴BC=6+![]() .
.
过点A作AM⊥BC于点M,
∵∠B=60°,AB=CD=6,
∴∠BAM=30°,
∴BM=3,
∴AM=![]() BM=
BM=![]() ,
,
∴平行四边形ABCD的面积=(6+![]() )×
)×![]() =18
=18![]() +9;
+9;
(2)过点C作CN⊥EQ于点N,其延长线交AD于点K,
∵∠EQC=45°,
∴△CNQ为等腰直角三角形,
∴∠NQC=∠NCQ=45°,且CQ=![]() CN,
CN,
∵HE=HF,
∴∠HEF=∠HFE,
∵FG⊥AB,CN⊥EQ,
∴∠FGB=∠ENC=90°,
又∵BE=CF,
∴BF=CE,
∴△BGF≌△CNE(AAS),
∴BG=CN,∠B=∠ECN,
∴CQ=![]() BG,
BG,
又∵AC=BC=AD,
∴∠D=∠ACD,
又∵∠B=∠D,
∴∠ECN=∠ACD,
∴∠KAC=∠BCA=∠NCQ=45°,
∴∠BAC=∠ACD=∠B=∠CDA=∠ECN =67.5°,
∴∠ACK= ∠ECN-∠BCA =22.5°,∠QEC=180°-90°-∠ECN =22.5°,
即:∠ACK=∠QEC,
又∵∠KAC=∠CQE=45°,AC=QE,
∴△ACK≌△QEC(ASA),
∴CK=CE,
∵∠CDA=67.5°,∠NCQ=45°,
∴∠CKD=180°-45°-67.5°=67.5°,
∴∠CKD=∠CDA,
∴CK=CD,
∴CE=CD,
∵CD=CQ+QD=![]() BG+DQ,
BG+DQ,
∴![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=2cm,BC=3cm,点P沿B→A→D运动,运动到点D时停止运动,点P运动的同时,另一点Q从B→C运动,速度是点P的一半,当点P停止运动时,点Q也停止运动.设点P运动的路程为xcm,其中设
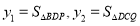 ,可可根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是可可的探究过程,请补充完整.
,可可根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是可可的探究过程,请补充完整.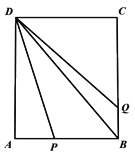
(1)如图是画出的函数
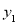 与x的函数图象,观察图象.当x=1时,
与x的函数图象,观察图象.当x=1时,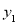 =_____;并写出函数的一条性质:________________________________________.
=_____;并写出函数的一条性质:________________________________________.(2)请帮助可可写出
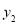 与x的函数关系式(不用写出取值范围)__________________.
与x的函数关系式(不用写出取值范围)__________________.(3)请按照列表、描点、连线的步骤在同一直角坐标系中,画出函数
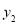 的图象.
的图象.(4)结合画出函数图象,解决问题:当
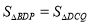 时,点P运动的路程x=_______.
时,点P运动的路程x=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
类型 价格
进价(元/盏)
售价(元/盏)
A型
25
45
B型
40
70
(1)若商场进货款为3100元,则这两种台灯各购进多少盏?
(2)若商场在3200元的限额内购进这两种台灯,且A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
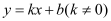 的图象与x轴、y轴分别交于A、B两点,且与反比例函数
的图象与x轴、y轴分别交于A、B两点,且与反比例函数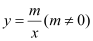 的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,
的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,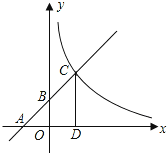
(1)求点A,B,D的坐标;
(2)求一次函数和反比例函数的解析式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
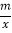 的图象交于点A﹙﹣2,﹣5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙﹣2,﹣5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.(1)求反比例函数y=
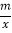 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;(2)连接OA,OC.求△AOC的面积.
(3)当kx+b>
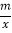 时,请写出自变量x的取值范围.
时,请写出自变量x的取值范围.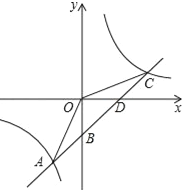
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=kx+b与x轴、y轴分别交于A,B两点,其中点B的坐标为(0,6),∠BAO=30°将直线l1沿着y轴正方向平移一段距离得到直线l2交y轴于点M,且l1与l2之间的距离为3,点C(x,y)是直线11上的一个动点,过点C作AB的垂线CD交y轴于点D.
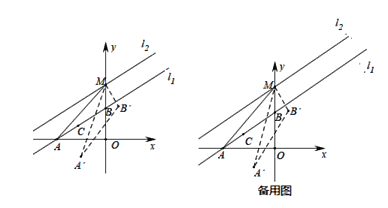
(1)求点M的坐标和直线l1的解析式;
(2)当C运动到什么位置时,△AOD的面积为21
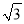 ,求出此时点C的坐标;
,求出此时点C的坐标;(3)连接AM,将△ABM绕着点M旋转得到△A'B'M,在平面内是否存在一点N.使四边形AMA'N为矩形?若存在,求出点N的坐标:若不存在,请说明理由.
相关试题

