【题目】如图,已知△ABC是等边三角形,以AC为直径的⊙O分别交AB,BC于点D,E,点F在AB的延长线上,2∠BCF=∠BAC. 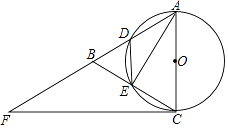
(1)求∠ADE的度数.
(2)求证:直线CF是⊙O的切线.
参考答案:
【答案】
(1)解:∵△ABC是等边三角形,
∴∠ACB=∠ACE=60°,
∴∠ADE=180°﹣∠ACE=120°

(2)解:∵⊙O的直径是AC,
∴∠AEC=90°,即AE⊥BC.
又∵AB=AC,
∴∠BAE=∠CAE.
∵2∠BCF=∠BAC,
∴∠BCF=∠CAE.
∵∠CAE+∠ECA=90°,
∴∠BCF+∠ECA=90°,即∠ACF=90°.
又AC是直径,
∴直线CF是⊙O的切线
【解析】(1)根据圆内接四边形的对角互补可以求得∠ADE的度数.(2)欲证明直线CF是⊙O的切线,只需推知∠ACF=90°.
【考点精析】掌握等边三角形的性质和圆周角定理是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲同学手中藏有三张分别标有数字
 ,
,  ,1的卡片,乙同学手中藏有三张分别标有1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
,1的卡片,乙同学手中藏有三张分别标有1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果.
(2)现制定这样一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则称甲获胜;否则称乙获胜.请问这样的游戏规则公平吗?请你用概率知识解释. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
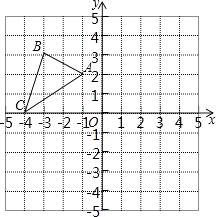
(1)画出△ABC关于原点O的中心对称图形△A1B1C1;
(2)画出将△ABC绕点A逆时针旋转90°得到△AB2C2 ,
(3)△A1B1C1中顶点A1坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校要将一块长为a米,宽为b米的长方形空地设计成花园,现有如下两种方案供选择.
方案一:如图1,在空地上横、竖各铺一条宽为4米的石子路,其余空地种植花草.
方案二:如图2,在长方形空地中留一个四分之一圆和一个半圆区域种植花草,其余空地铺筑成石子路.
(1) 分别表示这两种方案中石子路(图中阴影部分)的面积(若结果中含有π,则保留)
(2) 若a=30,b=20,该校希望多种植物美化校园,请通过计算选择其中一种方案(π取3.14).

-
科目: 来源: 题型:
查看答案和解析>>【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一张长方形纸条上画一条数轴.

(1)若折叠纸条,数轴上表示﹣3的点与表示5的点重合,则折痕与数轴的交点表示的数为 ;
(2)若将此纸条沿图中虚线处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折2次后,再将其展开,则最左端的折痕和最右端的折痕与数轴的交点表示的数分别是 ;
(3)如果该数轴上的两个点表示的数为a和b,经过对折,两点恰好重合,则折痕与数轴的交点表示的数为 ;(用含a,b的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )

A. 2
 cm B. 3
cm B. 3 cm C. 4
cm C. 4 cm D. 3cm
cm D. 3cm
相关试题

