【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“快乐分式”.如:![]() ,则
,则 ![]() 是“快乐分式”.
是“快乐分式”.
(1)下列式子中,属于“快乐分式”的是 (填序号);
①![]() ,②
,② ![]() ,③
,③![]() ,④
,④ ![]() .
.
(2)将“快乐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() = .
= .
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
参考答案:
【答案】(1)①②③;(2)![]() ;(3)
;(3)![]() ,x=-3
,x=-3
【解析】
(1)根据快乐分式的定义分析即可;
(2)根据快乐分式的定义变形即可;
(3)先化简,再根据快乐分式的定义变形,然后再根据x的值和分式的值为整数讨论即可.
解:(1)①![]() ,是快乐分式 ,
,是快乐分式 ,
② ![]() ,是快乐分式,
,是快乐分式,
③![]() ,是快乐分式,
,是快乐分式,
④ ![]() 不是分式,故不是快乐分式.
不是分式,故不是快乐分式.
故答案为:①②③ ;
(2) 原式=![]() =
=![]() ;
;
(3)原式=![]()
=![]() =
= ![]()
= ![]() =
=![]()
∵当![]() 或
或 ![]() 时,分式的值为整数,
时,分式的值为整数,
∴x的值可以是0或![]() 或1或
或1或![]() ,
,
又∵分式有意义时,x的值不能为0、1、![]() ,
,
∴ ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
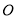 是直线
是直线 上一点,
上一点, 为任一条射线,
为任一条射线, 平分
平分 ,
, 平分
平分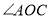 .
.
(1)找出图中
 的补角,
的补角,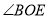 的补角;
的补角;(2)若
 ,求
,求 和
和 的度数;
的度数;(3)
 与
与 具有怎样的数量关系?说明理由.
具有怎样的数量关系?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个菱形的两个顶点与一个正方形的两个顶点重合,并且这两个四边形没有公共边,菱形的面积为24cm2,正方形的面积为32cm2,则菱形的边长为______________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线
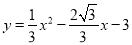 与x轴交于A、B两点(点A在点B左侧),与y轴交于C点,点E在第一象限且四边形ACBE为矩形.
与x轴交于A、B两点(点A在点B左侧),与y轴交于C点,点E在第一象限且四边形ACBE为矩形.(1)求∠BCE的度数;
(2)如图2,F为线段BC上一动点,P为第四象限内抛物线上一点,连接CP、FP、BP、EF,M,N分别是线段CP,FP的中点,连接MN,当△BCP面积最大,且MN+EF最小时,求PF的长度;
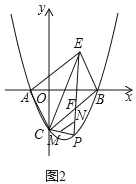
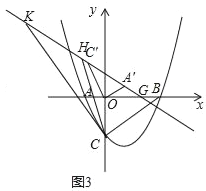
(3)如图3,将△AOC绕点O顺时针旋转一个角度α(0°<α<180°),点A,C的对应点分别为A',C',直线A'C'与x轴交于点G,G在x轴正半轴上且OG=
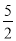 .线段KH在直线A'C'上平移( K在H左边),且KH=5,△KHC是否能成为等腰三角形?若能,请求出所有符合条件的点K的坐标;若不能,请说明理由.
.线段KH在直线A'C'上平移( K在H左边),且KH=5,△KHC是否能成为等腰三角形?若能,请求出所有符合条件的点K的坐标;若不能,请说明理由.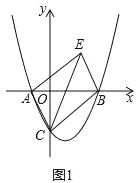
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,某超市从一楼到二楼的电梯
 的长为16. 50 m,坡角
的长为16. 50 m,坡角 为32°.
为32°.(1)求一楼与二楼之间的高度
 (精确到0. 01 m) ;
(精确到0. 01 m) ;(2)电梯每级的水平级宽均是0.25m,如图②,小明跨上电梯时,该电梯以每秒上升2级
的高度运行,10s后他上升了多少米?
(精确到0. 01 m,参考数据:
 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2018春季环境整治活动中,某社区计划对面积为1600m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y关于x的函数关系式;
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=50°,过点O引射线OC,若∠AOC:∠BOC=2:3,OD平分∠AOB,求∠COD的度数.
相关试题

