【题目】如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF交于点D,则下列结论中不正确的是( )
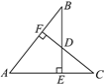
A. △ABE≌△ACF B. 点D在∠BAC的平分线上
C. △BDF≌△CDE D. D是BE的中点
参考答案:
【答案】D
【解析】
由题, BE⊥AC于E,CF⊥AB于F,∴∠AFC=∠AEB=90°,故在Rt△AEB中,∠B=90°-∠A, 在Rt△AFC中∠C=90°-∠A,∴∠B=∠C,在△ABE和△ACF中,∠A=∠A, AB = AC,∠B=∠C,∴△ABE≌△ACF(ASA),故A选项正确,∵△ABE≌△ACF,∴AE=AF,AC=AB,连接AD,在Rt△AFD和Rt△AED中, AE=AF,AD=AD,∴Rt△AFD≌Rt△AED(HL),∠DAF=∠DAE,即点D在∠BAC的平分线上,选项B正确,由AE=AF,AC=AB,得BF=CE,在△BDF和△CDE中,∠BFD=∠CED=90°,∠B=∠C, BF=CE,∴△BDF≌△CDE,选项C正确,而点D不一定是BE的中点,故选D.
试题全等三角形的判定方法有:1.边边边(SSS);2.边角边(SAS);3.角角边(AAS);4.角边角(ASA);5.直角三角形中的斜边直角边(HL);两三角形全等,对应边相等,对应角相等,由题, BE⊥AC于E,CF⊥AB于F,∴∠AFC=∠AEB=90°,故在Rt△AEB中,∠B=90°-∠A, 在Rt△AFC中∠C=90°-∠A,∴∠B=∠C,在△ABE和△ACF中,∠A=∠A, AB = AC,∠B=∠C,∴△ABE≌△ACF(ASA),故A选项正确,∵△ABE≌△ACF,∴AE=AF,AC=AB,连接AD,在Rt△AFD和Rt△AED中, AE=AF,AD=AD,∴Rt△AFD≌Rt△AED(HL),∠DAF=∠DAE,即点D在∠BAC的平分线上,选项B正确,由AE=AF,AC=AB,得BF=CE,在△BDF和△CDE中,∠BFD=∠CED=90°,∠B=∠C, BF=CE,∴△BDF≌△CDE,选项C正确,而点D不一定是BE的中点,故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华在某月的日历上圈出相邻的四个数,算出这四个数字的和为
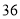 ,那么这四个数在日历上位置的形式是( )
,那么这四个数在日历上位置的形式是( )A.
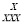 B.
B.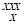 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,七年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,“爱国”主题所对应的圆心角是多少;
(4)如果该校七年级共有
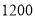 名学生,请估计该校选择以“友善”为主题的七年级学生有多少名.
名学生,请估计该校选择以“友善”为主题的七年级学生有多少名. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形ABCD的边长为4
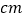 ,E、F分别是BC、DC边上一动点,E、F同时从点C均以1
,E、F分别是BC、DC边上一动点,E、F同时从点C均以1  的速度分别向点B、点D运动,当点E与点B重合时,运动停止.设运动时间为
的速度分别向点B、点D运动,当点E与点B重合时,运动停止.设运动时间为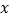 (
(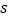 ),运动过程中△AEF的面积为
),运动过程中△AEF的面积为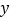 ,请写出用
,请写出用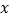 表示
表示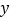 的函数关系式,并写出自变量
的函数关系式,并写出自变量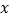 的取值范围.
的取值范围.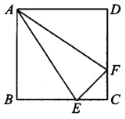
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,完成下列题目:
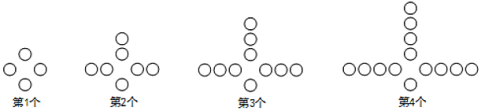
(1)填写下表:
图案序号
1
2
3
4
…
○个数
4
7
…
(2)若按上面的规律继续摆放,是否存在第
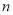 个图形,其中恰好含有2020个○?
个图形,其中恰好含有2020个○? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( )
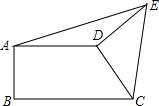
A.1 B.2 C.5 D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】为实施乡村振兴战略,解决某山区老百姓出行难的问题,当地政府决定修建一条高速公路.其中一段长为146米的山体隧道贯穿工程由甲乙两个工程队负责施工.甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26米.已知甲工程队每天比乙工程队多掘进2米,按此速度完成这项隧道贯穿工程,甲乙两个工程队还需联合工作多少天?
相关试题

