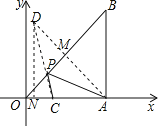
【题目】如图,在平面直角坐标系中,等腰Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,3),点C的坐标为(1,0),点P为斜边OB上的一个动点,则PA+PC的最小值为_____.

参考答案:
【答案】![]()
【解析】
作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,求出AM,求出AD,求出DN、CN,根据勾股定理求出CD,即可得出答案.
解:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,
则此时PA+PC的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵B(3,3),
∴AB=3,OA=3,∠B=45°,由勾股定理得:OB=3![]() ,
,
∴AM=![]() OB=
OB=![]() ,
,
∴AD=2AM=3![]() ,
,
∵∠AMB=90°,∠B=45°,
∴∠BAM=45°,
∵∠BAO=90°,
∴∠OAM=45°,
∵DN⊥OA,
∴∠NDA=45°,
∴AN=DN=![]() AD=3
AD=3
∵C(1,0),
∴CN=1,
在Rt△DNC中,由勾股定理得:DC=![]() =
=![]() ,
,
即PA+PC的最小值是![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写推理理由
如图:EF∥AD,∠1=∠2,∠BAC=70°,把求∠AGD的过程填写完整.

证明:∵EF∥AD
∴∠2= ( )
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
又∵∠BAC=70°
∴∠AGD=
-
科目: 来源: 题型:
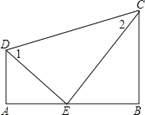
查看答案和解析>>【题目】已知:如图,DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°.试猜想BC与AB有怎样的位置关系,并说明其理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
①
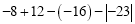
②
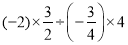
③12-7×(-4)+8÷(-2)
④
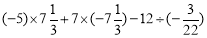
⑤33
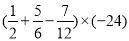
⑥-14+(0.5-2)
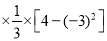
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划租用6辆客车送一批师生参加一年一度的哈尔滨冰雕节,感受冰雕艺术的魅力.现有甲、乙两种客车,它们的载客量和租金如下表.设租用甲种客车x辆,租车总费用为y元.
甲种客车
乙种客车
载客量(人/辆)
45
30
租金(元/辆)
280
200
(1)求出y(元)与x(辆)之间的函数关系式,指出自变量的取值范围;
(2)若该校共有240名师生前往参加,领队老师从学校预支租车费用1650元,试问预支的租车费用是否可以结余?若有结余,最多可结余多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 的对角线
的对角线 相交于点
相交于点 .
.
(1)求证:四边形
 为菱形;
为菱形;(2)
 垂直平分线段
垂直平分线段 于点
于点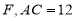 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是正方形
是正方形 对角线
对角线 上一点,
上一点, 于
于 ,点
,点 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)求证:
 ;
;(2)当点
 在对角线
在对角线 (不含
(不含 、
、 两点)上运动时,
两点)上运动时, 是否为定值?如果是,请求其值;如果不是,试说明理由.
是否为定值?如果是,请求其值;如果不是,试说明理由.
相关试题

