Question

【题目】如图1，点O为直线AB上一点，过O点作射线OC，使∠AOC:∠BOC=1:2，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线的下方.

（1）将图1中的三角板绕点O按逆时针方向旋转至图2的位置，使得ON落在射线OB上，此时三角板旋转的角度为____________度；

（2）在上述直角三角板从图1逆时针旋转到图3的位置的过程中，若三角板绕点O按15°每秒的速度旋转，当直角三角板的直角边ON所在直线恰好平分∠AOC时，求此时三角板绕点O的运动时间t的值.

（3）将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中，假如第t秒时，OA、OC、ON三条射线构成相等的角，求此时t的值为多少？（直接写出答案）

Answer 1

【答案】（1）90；（2）4或16秒；（3）t的值为6、15、24、33.

【解析】试题分析：（1）由∠MON=90°即可得出结论；

（2）分两种情况讨论即可；

（3）分四种情况讨论即可．

试题解析：解：（1）90；

（2）（i）如图，

当直角边ON在∠AOC外部时，由直线ON平分∠AOC，可得∠BON=30°．因此三角板绕点O逆时针旋转60°．此时三角板的运动时间为：t=60°÷15°=4（秒）．

（ⅱ）如图，当直角边ON在∠AOC内部时，由直线ON平分∠AOC，可得∠CON=30°．

因此三角板绕点O逆时针旋转240°．此时三角板的运动时间为：t=240°÷15°=16（秒）．

∴当三角板绕点O运动了4秒或16秒时，直角三角板的直角边ON所在直线恰好平分∠AOC．

（3）∵∠AOC：∠BOC=1：2，∴∠AOC=60°，∠BOC=120°．

①如图①，当∠AON=∠NOC时，此时∠AON=(360°－60°)÷2=150°，t=(150°－90°)÷10°=6（秒）；

②如图②，当∠NOC=60°时，此时旋转的度数为：90°+60°=150°，t=150°÷10°=15（秒）；

③如图③，当ON平分∠AOC时，此时t=(90°+120°+30°)÷10=24（秒）

④如图④，当∠AON=∠AOC时，此时t=(90°+180°+60°)÷10=33（秒）

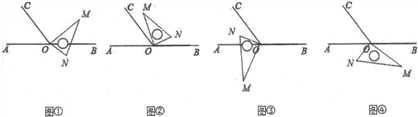
故t的值为6、15、24、33．