【题目】如图,点A,B,C,D在一条直线上,△ABF≌△DCE.你能得出哪些结论?(请写出三个以上的结论)
参考答案:
【答案】解:∵△ABF≌△DCE
∴∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;
∴AF∥ED,AC=BD,BF∥CE
【解析】根据全等三角形对应角相等,对应边相等得出∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;再根据平行线的判定定理及等式的性质得出AF∥ED,AC=BD,BF∥CE。
【考点精析】掌握平行线的判定和全等三角形的性质是解答本题的根本,需要知道同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;全等三角形的对应边相等; 全等三角形的对应角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第 2020 秒时跳蚤所在位置的坐标是( )

A.(5,44)B.(4,44)C.(4,45)D.(5,45)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点 D 是边 BC 上的点(与 B、C 两点不重合),过点 D作 DE∥AC,DF∥AB,分别交 AB、AC 于 E、F 两点,下列说法正确的是( )
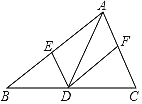
A. 若 AD 平分∠BAC,则四边形 AEDF 是菱形
B. 若 BD=CD,则四边形 AEDF 是菱形
C. 若 AD 垂直平分 BC,则四边形 AEDF 是矩形
D. 若 AD⊥BC,则四边形 AEDF 是矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,对于点
中,对于点 ,若点
,若点 的坐标为
的坐标为 ,则称点
,则称点 是点
是点 的“
的“ 演化点”.例如,点
演化点”.例如,点 的“
的“ 演化点”为
演化点”为 ,即
,即 .
.(1)已知点
 的“
的“ 演化点”是
演化点”是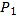 ,则
,则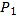 的坐标为________;
的坐标为________;(2)已知点
 ,且点
,且点 的“
的“ 演化点”是
演化点”是 ,则
,则 的面积
的面积 为__________;
为__________;(3)己知
 ,
,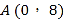 ,
, ,
, ,且点
,且点 的“
的“ 演化点”为
演化点”为 ,当
,当 时,
时, ___________.
___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形 ABCD中,对角线 AC 与 BD 相交于点 O,过点 A作 BD的垂线,垂足为 E.已知∠EAD=3∠BAE,求∠EAO 的度数( )

A.22.5°B.67.5°C.45°D.60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月全国两会胜利召开,某数学兴趣小组就两会期间出现频率最高的热词:A脱贫攻坚.B.绿色发展.C.自主创新.D.简政放权等热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了名同学;
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角的度数是;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注.某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请根据统计图中所提供的信息解答下列问题:
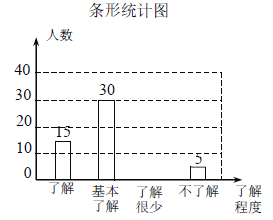
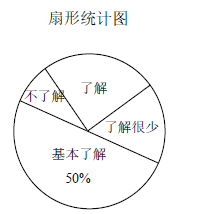
(1)接受问卷调查的学生共有 人;
(2)扇形统计图中“了解”部分所对应扇形的圆心角为 度;
(3)请补全条形统计图;
(4)若该中学共有学生1200人,则该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数约为多少人?
相关试题

