【题目】“校园安全”受到全社会的广泛关注.某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请根据统计图中所提供的信息解答下列问题:
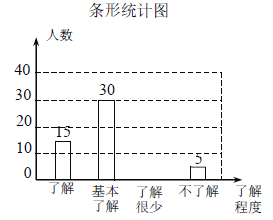
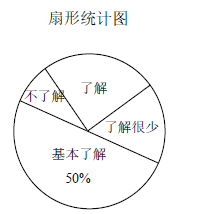
(1)接受问卷调查的学生共有 人;
(2)扇形统计图中“了解”部分所对应扇形的圆心角为 度;
(3)请补全条形统计图;
(4)若该中学共有学生1200人,则该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数约为多少人?
参考答案:
【答案】(1)60;(2)90;(3)补全图形见解析;(4)900人
【解析】
(1)由基本了解的有30人,占50%,可求得接受问卷调查的学生数,
(2)利用扇形统计图中“了解”部分所占的百分比乘以![]() 即可得到答案;
即可得到答案;
(3)由(1)可求得了解很少的人数,继而补全条形统计图;
(4)利用样本估计总体的方法,即可求得答案.
解:(1)接受问卷调查的学生共有![]() 人.
人.
(2)扇形统计图中“了解”部分所对应扇形的圆心角为360°×![]() =90°,
=90°,
故答案为:60、90.
(3)“了解很少”的人数为60-(15+30+5)=10人, 补全图形如下:
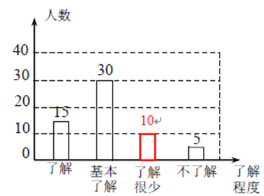
(4)估计该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数为:
1200× ![]() =900人.
=900人.
答:该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数约为900人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D在一条直线上,△ABF≌△DCE.你能得出哪些结论?(请写出三个以上的结论)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形 ABCD中,对角线 AC 与 BD 相交于点 O,过点 A作 BD的垂线,垂足为 E.已知∠EAD=3∠BAE,求∠EAO 的度数( )

A.22.5°B.67.5°C.45°D.60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月全国两会胜利召开,某数学兴趣小组就两会期间出现频率最高的热词:A脱贫攻坚.B.绿色发展.C.自主创新.D.简政放权等热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了名同学;
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角的度数是;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
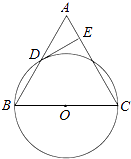
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB= ,求DE的长.
,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题

如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD= AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】现计划把甲种货物306吨和乙种货物230吨运往某地,已知有A、B两种不同规格的货车共50辆,如果每辆A型货车最多可装甲种货物7吨和乙种货物3吨,每辆B型货车最多可装甲种货物5吨和乙种货物7吨.
(1)装货时如何安排A、B两种货车的辆数,共有哪些方案?
(2)使用A型车每辆费用为600元,使用B型车每辆费用800元,上述方案中,哪个方案运费最省?最省的运费是多少元?
相关试题

