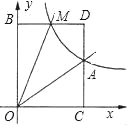
【题目】如图,已知正比例函数y=ax与反比例函数y=![]() 的图象交于点A(3,2)
的图象交于点A(3,2)
(1)求上述两函数的表达式;
(2)M(m,n)是反比例函数图象上的一个动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A点作直线AC∥y轴交x轴于点C,交直线MB于点D.若s四边形OADM=6,求点M的坐标,并判断线段BM与DM的大小关系,说明理由;
(3)探索:x轴上是否存在点P.使△OAP是等腰三角形?若存在,求出点P的坐标; 若不存在,说明理由.
参考答案:
【答案】(1)反比例函数的表达式为:y=![]() ,正比例函数的表达式为y=
,正比例函数的表达式为y=![]() x;(2)BM=DM;(3)存在,(
x;(2)BM=DM;(3)存在,(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(6,0)或(
,0)或(6,0)或(![]() ,0)
,0)
【解析】
(1)将A(3,2)分别代入y=![]() ,y=ax中,得ak的值,进而可得正比例函数和反比例函数的表达式;
,y=ax中,得ak的值,进而可得正比例函数和反比例函数的表达式;
(2)由S△OMB=S△OAC=![]() |k|=3,可得S矩形OBDC=12;即OCOB=12;进而可得mn的值,故可得BM与DM的大小;比较可得其大小关系;
|k|=3,可得S矩形OBDC=12;即OCOB=12;进而可得mn的值,故可得BM与DM的大小;比较可得其大小关系;
(3)存在.由(2)可知D(3,4),根据矩形的性质得A(3,2),分为OA为等腰三角形的腰,OA为等腰三角形的底,分别求P点坐标.
解:(1)将A(3,2)分别代入y=![]() ,y=ax中,得:2=
,y=ax中,得:2=![]() ,3a=2
,3a=2
∴k=6,a=![]() ,
,
∴反比例函数的表达式为:y=![]() ,
,
正比例函数的表达式为y=![]() x;
x;
(2)BM=DM
理由:∵S△OMB=S△OAC=![]() ×|k|=3
×|k|=3
∴S矩形OBDC=S四边形OADM+S△OMB+S△OAC=3+3+6=12
即OCOB=12
∵OC=3
∴OB=4
即n=4
∴m=![]() =
=![]() ,即点M的坐标为(
,即点M的坐标为(![]() ,4)
,4)
∴MB=![]() ,MD=3﹣
,MD=3﹣![]() =
=![]() ,
,
∴MB=MD;
(3)存在.
由(2)得A(3,2),OA=![]()
当OA为等腰三角形的腰时,P(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(6,0),
,0)或(6,0),
当OA为等腰三角形的底,P(![]() ,0).
,0).
∴满足条件的P点坐标为(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(6,0)或(
,0)或(6,0)或(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:我们知道a的几何意义是在数轴上数a对应的点与原点的距离.数轴上数a与数0对应点之间的距离,
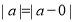 这 个结论可以推广为: |a- b|均表示在数轴上数a与b对应点之间的距离,例:已知|a-1|=2, 求a的值.
这 个结论可以推广为: |a- b|均表示在数轴上数a与b对应点之间的距离,例:已知|a-1|=2, 求a的值.解:在数轴上与1的距离为2点的对应数为3和-1,即a的值为3和-1.
仿照阅读材料的解法,解决下列问题
(1)已知
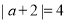 ,求a的值.
,求a的值.(2)若数轴上表示a的点在-4与2之间,则|a+4|+|a-2|的值为___
(3)当a满足什么条件时,|a-1|+ |a+2|有最小值,最小值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元,厂方开展促销活动期间,向客户提供两种优惠方法:①买一套西装送一条领带;②西装和领带均按定价的90%付款。某商店到该服装厂购买西装20件,领带若干条.
(1)领带买多少条时,两种优惠方法相同?
(2)购买50条领带时,应采用哪一种方案更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示.
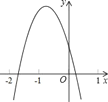
下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l为y=
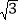 x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).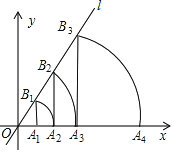
-
科目: 来源: 题型:
查看答案和解析>>【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
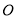 是直线
是直线 上的一点,将一直角三角板如图摆放,过点
上的一点,将一直角三角板如图摆放,过点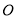 作射线
作射线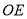 平分
平分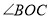 .当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现
.当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现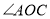 与
与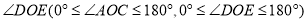 之间有怎样的数量关系?
之间有怎样的数量关系?(1)如图1,当
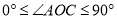 时,若
时,若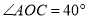 ,求
,求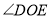 的度数;
的度数;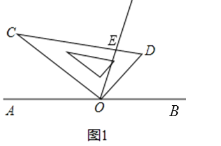
(2)如图2,当
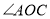 是钝角时,使得直角边
是钝角时,使得直角边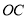 在直线
在直线 的上方,若
的上方,若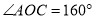 ,其他条件不变,直接写出
,其他条件不变,直接写出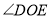 的度数;
的度数;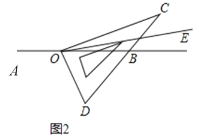
(3)若
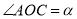 ,在旋转过程中你发现
,在旋转过程中你发现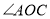 与
与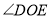 之间有怎样的数量关系?请你直接用含
之间有怎样的数量关系?请你直接用含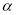 的代数式表示
的代数式表示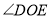 的度数;
的度数;
相关试题

