【题目】已知二次函数y=ax2+bx+c的图象如图所示.
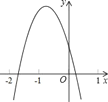
下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】D
【解析】∵抛物线开口向下,∴a<0.
∵抛物线的对称轴在y轴的左侧, ![]() ,∴b<0.
,∴b<0.
∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc>0,故①正确;
![]() ,∴2a﹣b<0,故②正确;
,∴2a﹣b<0,故②正确;
∵当x=﹣2时,y<0,∴4a﹣2b+c<0,故③正确;
∵当x=﹣1时,y>0,∴a﹣b+c>0.
∵当x=1时,y<0,∴a+b+c<0.
∴(a﹣b+c)(a+b+c)<0,即(a+c﹣b)(a+c+b)<0,∴(a+c)2﹣b2<0,故④正确.
所以正确的个数有4个.故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A样本的数据如下:72,73,76,76,77,78,78,78,B样本的数据恰好是A样本数据每个都加2,则A,B两个样本的下列统计量对应相同的是( )
A.平均数
B.标准差
C.中位数
D.众数 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.
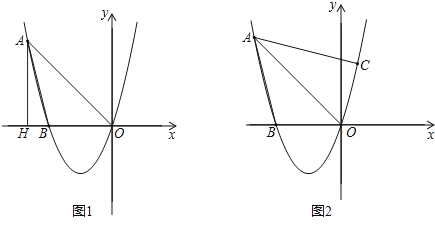
-
科目: 来源: 题型:
查看答案和解析>>【题目】从扬州乘“K”字头列车A、“T”字头列车B都可直达南京,已知A车的平均速度为60km/h,B车的平均速度为A车的1.5倍,且走完全程B车所需时间比A车少45分钟.
(1)求扬州至南京的铁路里程;
(2)若两车以各自的平均速度分别从扬州、南京同时相向而行,问经过多少时间两车相距15km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,EF∥AB,∠1=50°,CE=3,EF比CF大1,则EF的长为( )
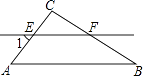
A.5
B.6
C.3
D.4 -
科目: 来源: 题型:
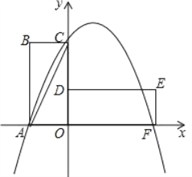
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=1,tan∠ACB=2,将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF.点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,抛物线y=ax2+bx+2的图象过点A,C,F.
(1)求抛物线所对应函数的表达式;
(2)在边DE上是否存在一点M,使得以O,D,M为顶点的三角形与△ODE相似,若存在,求出经过M点的反比例函数的表达式,若不存在,请说明理由;
(3)在x轴的上方是否存在点P,Q,使以O,F,P,Q为顶点的平行四边形的面积是矩形OABC面积的2倍,且点P在抛物线上,若存在,请求出P,Q两点的坐标;若不能存在,请说明理由;
(4)在抛物线的对称轴上是否存在一点H,使得HA﹣HC的值最大,若存在,直接写出点H的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这2名学生立定跳远成绩的( )
A.方差B.平均数C.频率分布D.众数
相关试题

