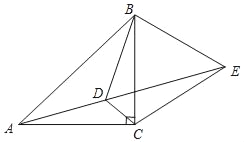
【题目】如图,点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上一点,且CE=CA,给出以下结论:①DE平分∠BDC; ②△BCE是等边三角形;③∠AEB=45°;④DE=AD+CD;正确的结论有_____.(请填序号)
参考答案:
【答案】①②③④.
【解析】
①先根据等腰直角三角形的性质及已知条件得出∠DAB=∠DBA=30°,则AD=BD,再证明CD是边AB的垂直平分线,得出∠ACD=∠BCD=45°,然后根据三角形外角的性质求出∠CDE=∠BDE=60°即可;
②先利用等角对等边证BC=CE,再推得∠BCE=60°可得结论;
③利用差可求得结论:∠AEB=∠BEC-∠AEC;
④截取DG=DC,证明△DCG是等边三角形,再证明△ACD≌△ECG,利用线段的和与等量代换可得结论.
解:①∵△ABC是等腰直角三角形,∠ACB=90°,
∴∠BAC=∠ABC=45°,
∵∠CAD=∠CBD=15°,
∴∠BAD=∠ABD=45°-15°=30°,
∴BD=AD,
∴D在AB的垂直平分线上,
∵AC=BC,
∴C也在AB的垂直平分线上,
即直线CD是AB的垂直平分线,
∴∠ACD=∠BCD=45°,
∴∠CDE=∠CAD+∠ACD=15°+45°=60°,
∵∠BDE=∠DBA+∠BAD=60°;
∴∠CDE=∠BDE,
即DE平分∠BDC;
所以①正确;
②∵CA=CB,CA=CE,
∴CB=CE,
∵∠CAD=∠AEC=15°,
∴∠ACE=180°-15°-15°=150°,
∵∠ACB=90°,
∴∠BCE=150°-90°=60°,
∴△BCE是等边三角形;
所以②正确;
③∵△BCE是等边三角形,
∴∠BEC=60°,
∵∠AEC=15°,
∴∠AEB=60°-15°=45°,
所以③正确;
④在DE上取一点G,使DC=DG,连接CG,
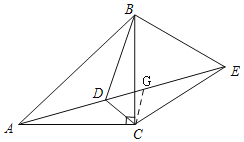
∵∠EDC=60°,
∴△DCG是等边三角形,
∴DC=DG=CG,∠DCG=60°,
∴∠GCE=150°-60°-45°=45°,
∴∠ACD=∠GCE=45°,
∵AC=CE,
∴△ACD≌△ECG,
∴EG=AD,
∴DE=EG+DG=AD+DC,
所以④正确;
正确的结论有:①②③④;
故答案为::①②③④.
-
科目: 来源: 题型:
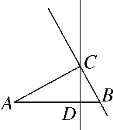
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发在直线BC上以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.当点E运动________s时,CF=AB.
-
科目: 来源: 题型:
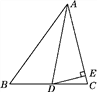
查看答案和解析>>【题目】在△ABC中,AD是角平分线,∠B=54°,∠C=76°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC,求∠EDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC=2
 ,若把Rt△ABC绕边AB所在直线旋转一周,则所得几何体的表面积为( )
,若把Rt△ABC绕边AB所在直线旋转一周,则所得几何体的表面积为( ) 
A.4π
B.4 π
π
C.8π
D.8 π
π -
科目: 来源: 题型:
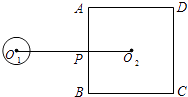
查看答案和解析>>【题目】如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现( )
A.3次
B.5次
C.6次
D.7次 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O在等边△ABC内,∠AOB=100°,∠BOC=x,将△BOC绕点C顺时针旋转60°,得△ADC,连接OD.
(1)△COD的形状是 ;
(2)当x=150°时,△AOD的形状是 ;此时若OB=3,OC=5,求OA的长;
(3)当x为多少度时,△AOD为等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=500,∠C=600,求∠DAE和∠BOA的度数。

相关试题

