【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.
(1)求二次函数y=﹣![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.

参考答案:
【答案】(1)抛物线的解析式为y=﹣![]() x2+
x2+![]() x﹣2;
x﹣2;
【解析】
试题分析:(1)根据当x=0和x=5时所对应的函数值相等,可得(5,c),根据待定系数法,可得函数解析式;
(2)联立抛物线与直线,可得方程组,根据解方程组,可得B、C点坐标,根据勾股定理,可得AB的长;
(3)根据线段中点的性质,可得M点的坐标,根据旋转的性质,可得MN与BM的关系,根据平行四边形的判定,可得答案.
试题解析:(1)当x=0时,y=c,即(0,c).
由当x=0和x=5时所对应的函数值相等,得(5,c).
将(5,c)(1,0)代入函数解析式,得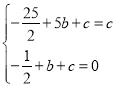 ,解得
,解得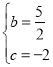 .
.
故抛物线的解析式为y=﹣![]() x2+
x2+![]() x﹣2;
x﹣2;
(2)联立抛物线与直线,得
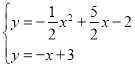 ,解得
,解得![]() ,
,![]() ,即B(2,1),C(5,﹣2).
,即B(2,1),C(5,﹣2).
由勾股定理,得AB=![]() =
=![]() ;
;
(3)如图:
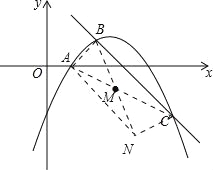 ,
,
四边形ABCN是平行四边形,∵M是AC的中点,∴AM=CM.
∵点B绕点M旋转180°得到点N,∴BM=MN,
∴四边形ABCN是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两圆的半径分别是3和4,圆心距的长为1,则两圆的位置关系为( )
A.外离
B.相交
C.内切
D.外切 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,⊙O的半径为1,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若点P与圆心O重合,则SP为⊙O的半径长;若点P与圆心O不重合,作射线OP交⊙O于点A,则SP为线段AP的长度.
图1为点P在⊙O外的情形示意图.
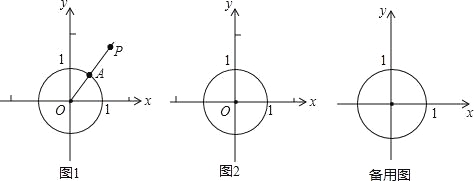
(1)若点B(1,0),C(1,1),D(0,
 ),则SB= ;SC= ;SD= ;
),则SB= ;SC= ;SD= ;(2)若直线y=x+b上存在点M,使得SM=2,求b的取值范围;
(3)已知点P,Q在x轴上,R为线段PQ上任意一点.若线段PQ上存在一点T,满足T在⊙O内且ST≥SR,直接写出满足条件的线段PQ长度的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣4÷ ﹣(﹣
﹣(﹣  )×(﹣30)
)×(﹣30)
(2)﹣20+(﹣14)﹣(﹣18)﹣13
(3)﹣22+|5﹣8|+24÷(﹣3)×
(4)﹣5m2n+4mn2﹣2mn+6m2n+3mn. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连结EC.如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图1,请你判断线段CE、BD之间的位置和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2画出图形,判断①中的结论是否仍然成立,并证明你的判断.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的三边长分别是5,x,7,第三边x的取值范围是_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据2,﹣4,x,6,﹣8的众数为6,则这组数据的中位数为______.
相关试题

