【题目】为丰富学生课余生活,我校准备开设兴趣课堂.为了了解学生对绘画、书法、舞蹈、乐器这四个兴趣小组的喜爱情况,在全校进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息尚不完整),请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中乐器部分的圆心角的度数;
(3)如果我校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的25名学生,估计书法兴趣小组至少需要准备多少名教师?
参考答案:
【答案】(1)200;(2)图详见解析,108°;(3)4.
【解析】
(1)根据参加绘画小组的人数是90,所占的百分比是45%,即可求得调查的总人数;
(2)利用360°乘以对应的比例即可求得圆心角的度数;
(3)利用样本估计总体的方法求出各书法兴趣小组的人数,再除以25即可解答.
(1)共有学生:90÷45%=200(人),
答:此次共调查了200名同学;
(2)喜爱乐器小组的人数是200-90-20-30=60(人);
扇形统计图中乐器部分的圆心角的度数是360°×![]() =108°.
=108°.

(3)学习书法有![]() ×1000=100(人),
×1000=100(人),
需要书法教师:100÷25=4(人),
答:估计书法兴趣小组至少需要准备4名教师.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L:y=﹣
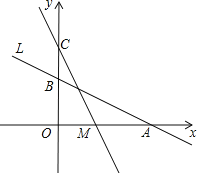
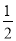 x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,请直接写出此时t值和M点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式6-2(x+1)≤3(x-2).
(2)解不等式组
 ,并写出该不等式组的整数解.
,并写出该不等式组的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).

(1)请在网格平面内作出平面直角坐标系;
(2)将△ABC平移至△DEF,使得A、B、C的对应点依次是D、E、F,已知D(2,3),请在网格中作出△DEF;
(3)若Q(a,b)是△DEF内一点,则△ABC内点Q的对应点点P的坐标是 (用a、b表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司现有A、B、C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1)写出所有选购方案(利用树状图或列表方法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
(3)现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示),恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有几台.

-
科目: 来源: 题型:
查看答案和解析>>【题目】人寿保险公司的一张关于某地区的生命表的部分摘录如下:
年龄
活到该年龄的人数
在该年龄的死亡人数
40
80500
892
50
78009
951
60
69891
1200
70
45502
2119
80
16078
2001
…
…
…
根据上表解下列各题:
(1)某人今年50岁,他当年去世的概率是多少?他活到80岁的概率是多少?
(保留三个有效数字)
(2)如果有20000个50岁的人参加人寿保险,当年死亡的人均赔偿金为10万元,预计保险公司需付赔偿的总额为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 的解析表达式为
的解析表达式为 ,且
,且 与
与 轴交于点
轴交于点 ,直线
,直线 经过点
经过点 ,直线
,直线 ,
,  交于点
交于点 .
.
(1)求点
 的坐标;
的坐标;(2)求直线
 的解析表达式;
的解析表达式;(3)求
 的面积;
的面积;(4)在直线
 上存在异于点
上存在异于点 的另一点
的另一点 ,使得
,使得 与
与 的面积相等,请直接写出点
的面积相等,请直接写出点 的坐标.
的坐标.
相关试题

