【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:①甲车行驶40千米开始休息②乙车行驶3.5小时与甲车相遇③甲车比乙车晚2.5小时到到B地④两车相距50km时乙车行驶了![]() 小时,其中正确的说法有( )
小时,其中正确的说法有( )
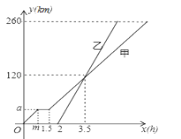
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】A
【解析】
根据“路程÷时间=速度”由函数图象就可以求出甲的速度,求出a的值和m的值解答①;根据函数图象可得乙车行驶3.5-2=1小时与甲车相遇解答②;再求出甲、乙车行驶的路程y与时间x之间的解析式解答③;由解析式之间的关系建立方程解答④.
由题意,得m=1.5-0.5=1,
120÷(3.5-0.5)=40(km/h),
则a=40,
∴甲车行驶40千米开始休息,
故①正确;
根据函数图象可得乙车行驶3.5-2=1.5小时与甲车相遇,故②错误;
当0≤x≤1时,设甲车y与x之间的函数关系式为y=k1x,
由题意,得:40=k1,
则y=40x,
当1<x≤1.5时,y=40;
当1.5<x≤7时,设甲车y与x之间的函数关系式为y=k2x+b,
由题意,得:![]() ,
,
解得:![]() ,
,
则y=40x-20;
设乙车行驶的路程y与时间x之间的解析式为y=k3x+b3,
由题意,得:![]() ,
,
解得:![]() ,
,
则y=80x-160;
当40x-20-50=80x-160时,解得:x=![]() ,
,
当40x-20+50=80x-160时,解得:x=![]() ,
,
![]() -2=
-2=![]() ,
,![]() -2=
-2=![]() ,
,
所以乙车行驶小时![]() 或
或![]() 小时,两车恰好相距50km,
小时,两车恰好相距50km,
故④错误;
当1.5<x≤7时,甲车y与x之间的函数关系式为y=40x-20,
当y=260时,260=40x-20,
解得:x=7,
乙车行驶的路程y与时间x之间的解析式为y=80x-160,
当y=260时,260=80x-160,
解得:x=5.25,
7-5.25=1.75(小时)
∴甲车比乙车晚1.75小时到到B地,
故③错误;
∴正确的只有①,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A在函数y1=﹣
 (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别是边BC、AD上的点,有下列条件:
①AE∥CF;②BE=FD;③∠1=∠2;④AE=CF.
若要添加其中一个条件,使四边形AECF一定是平行四边形,则添加的条件可以是( )

A. ①②③④ B. ①②③ C. ②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学要证明命题“平行四边形的对边相等.”是正确的,他画出了图形,并写出了如下已知和不完整的求证.
已知:如图,四边形ABCD是平行四边形.
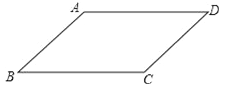
求证:AB=CD,
(1)补全求证部分;
(2)请你写出证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)化简:( ﹣
﹣  )÷
)÷  +
+ 
(2)计算:(﹣3)﹣2+ ﹣|1﹣2
﹣|1﹣2  |﹣(
|﹣( 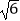 ﹣3)0 .
﹣3)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2﹣12x﹣28=0
(2)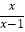 +
+ 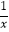 =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是______.

相关试题

