【题目】已知:|a+1|+(5﹣b)2+|c+2|=0且a、b、c分别是点A、B、C在数轴上对应的数.
(1)求a、b、c的值,并在数轴上标出A、B、C.
(2)若甲、乙、丙三个动点分别从A、B、C三点同时出发沿数轴负方向运动,它们的速度分别是![]() 、2、
、2、![]() (单位长度/秒),当乙追上丙时,乙是否追上了甲?为什么?
(单位长度/秒),当乙追上丙时,乙是否追上了甲?为什么?
(3)在数轴上是否存在一点P,使P到A、B、C的距离和等于10?若存在,请直接指出点P对应的数;若不存在,请说明理由.
![]()
参考答案:
【答案】(1) a=﹣1,b=5,c=﹣2;数轴表示见解析;(2)乙同时追上甲和丙,理由见解析;(3)当P对应的数是﹣![]() 或2时,P到A、B、C的距离和等于10.
或2时,P到A、B、C的距离和等于10.
【解析】
(1)根据非负数的性质即可求出a、b、c的值,在数轴上画出点A、B、C即可;
(2)设乙用x秒追上丙,根据追击问题的相等关系列出方程,求出x的值,再求出x秒时甲与乙在数轴上的位置,即可解决问题;
(3)分四种情形讨论:①当点P在点C左边时;②当点P在A、C之间时,PA+PB+PC<10,不存在;③当点P在A、B之间时;④当点P在点B右侧时,分别根据PA+PB+PC=10列出方程,即可解决问题.
(1)∵|a+1|+(5﹣b)2+|c+2|=0,
∴a+1=0,5﹣b=0,c+2=0,
∴a=﹣1,b=5,c=﹣2.
A、B、C三点在数轴上表示如下:
![]()
(2)当乙追上丙时,乙也刚好追上了甲.
由题意知道:AB=6,AC=1,BC=7.
设乙用x秒追上丙,
则![]()
解得:x=4.
则当乙追上丙时,甲运动了![]() 个单位长度,
个单位长度,
乙运动了2×4=8个单位长度,
此时恰好有AB+2=8,
故乙同时追上甲和丙;
(3)设点P对应的数为m,
①当点P在点C左边时,由题意,(5﹣m)+(﹣1﹣m)+(﹣2﹣m)=10,解得![]()
②当点P在A、C之间时,PA+PB+PC<10,不存在;
③当点P在A、B之间时,(5﹣m)+(m+1)+(m+2)=10,解得m=2,
④当点P在点B右侧时,(m﹣5)+(m+1)+(m+2)=10,解得m=4(不合题意舍去),
综上所述,当P对应的数是![]() 或2时,P到A、B、C的距离和等于10.
或2时,P到A、B、C的距离和等于10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3,点0是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 .
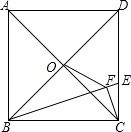
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连结CQ.若PA∶PB∶PC=3∶4∶5,连结PQ,试判断△PQC的形状( )

A. 直角三角形 B. 等腰三角形 C. 锐角三角形 D. 钝角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C,D,连接AC,BD.
(1)求出点C,D的坐标;
(2)设y轴上一点P(0,m),m为整数,使关于x,y的二元一次方程组
 有正整数解,求点P的坐标;
有正整数解,求点P的坐标;(3)在(2)的条件下,若Q点在线段CD上,横坐标为n,△PBQ的面积S△PBQ的值不小于0.6且不大于4,求n的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣14+3tan30°﹣
 +(2017+π)0+(
+(2017+π)0+(  )﹣2 .
)﹣2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的方格纸中,每一个小正方形的边长都为1.
(1)∠BCD是不是直角?请说明理由;
(2)求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

相关试题

