【题目】如图,已知一次函数y=kx+2的图象与x轴,y轴分别交于点A,B,与正比例函数y=![]() x交于点C,已知点C的横坐标为2,下列结论:①关于x的方程kx+2=0的解为x=3;②对于直线y=kx+2,当x<3时,y>0;③对于直线y=kx+2,当x>0时,y>2;④方程组
x交于点C,已知点C的横坐标为2,下列结论:①关于x的方程kx+2=0的解为x=3;②对于直线y=kx+2,当x<3时,y>0;③对于直线y=kx+2,当x>0时,y>2;④方程组![]() 的解为
的解为![]() ,其中正确的是( )
,其中正确的是( )

A. ①②③B. ①②④C. ①③④D. ②③④
参考答案:
【答案】B
【解析】
根据已知条件得到C(2,![]() ),把C(2,
),把C(2,![]() )代入y=kx+2得到y=﹣
)代入y=kx+2得到y=﹣![]() x+2,当x=0时,y=2,当y=0时,x=3,求得B(0,2),A(3,0),于是得到结论.
x+2,当x=0时,y=2,当y=0时,x=3,求得B(0,2),A(3,0),于是得到结论.
解:∵点C的横坐标为2,
∴当x=2时,y=![]() x=
x=![]() ,
,
∴C(2,![]() ),
),
把C(2,![]() )代入y=kx+2得,k=﹣
)代入y=kx+2得,k=﹣![]() ,
,
∴y=﹣![]() x+2,
x+2,
当x=0时,y=2,当y=0时,x=3,
∴B(0,2),A(3,0),
∴①关于x的方程kx+2=0的解为x=3,正确;
②对于直线y=kx+2,当x<3时,y>0,正确;
③对于直线y=kx+2,当x>0时,y<2,故③错误;
∵C(2,![]() ),
),
∴方程组![]() 的解为
的解为![]() ,正确;
,正确;
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是等腰Rt△ABC的外接圆,点D是
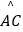 上的一点,BD交AC于点E,若BC=4,AD=
上的一点,BD交AC于点E,若BC=4,AD= 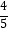 ,则AE的长是 .
,则AE的长是 . 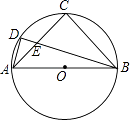
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D,E,F分别在三边上,且BE=CD,BD=CF,G为EF的中点.
(1)若∠A=40°,求∠B的度数;
(2)试说明:DG垂直平分EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某医药研究所开发一种新药,在做药效试验时发现,如果成人按规定剂量服用,那么服药后,每毫升血液中含药量y(μg)随时间t(h)的变化图象如图所示,根据图象回答:
(1)服药后几时血液中含药量最高?每毫升血液中含多少微克?
(2)在服药几时内,每毫升血液中含药量逐渐升高?在服药几时后,每毫升血液中含药量逐渐下降?
(3)服药后14 h时,每毫升血液中含药量是多少微克?
(4)如果每毫升血液中含药量为4微克及以上时,治疗疾病有效,那么有效时间为几时?

-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y1=
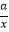 (a>0,a为常数)和y2=
(a>0,a为常数)和y2= 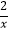 在第一象限内的图象如图所示,点M在y2=
在第一象限内的图象如图所示,点M在y2= 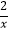 的图象上,MC⊥x轴于点C,交y1=
的图象上,MC⊥x轴于点C,交y1= 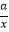 的图象于点A;MD⊥y轴于点D,交y1=
的图象于点A;MD⊥y轴于点D,交y1= 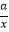 的图象于点B,当点M在y2=
的图象于点B,当点M在y2= 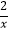 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积为2﹣a;
③当a=1时,点A是MC的中点;
④若S四边形OAMB=S△ODB+S△OCA , 则四边形OCMD为正方形.
其中正确的是 . (把所有正确结论的序号都填在横线上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(π﹣4)0+|3﹣tan60°|﹣(
 )﹣2+
)﹣2+ 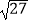 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠DCE=β.
(1)如图①,点D在线段BC上移动时,角α与β之间的数量关系是____________,请说明理由;
(2)如图②,点D在线段BC的延长线上移动时,角α与β之间的数量关系是____________,请说明理由;
(3)当点D在线段BC的反向延长线上移动时,请在图③中画出完整图形并猜想角α与β之间的数量关系是________________.

相关试题

