【题目】如图,在长方形 ![]() 中,
中, ![]() ,
, ![]() ,点
,点 ![]() 从点
从点 ![]() 出发,以
出发,以 ![]() 的速度沿
的速度沿 ![]() 向点
向点 ![]() 运动,设点
运动,设点 ![]() 的运动时间为
的运动时间为 ![]() 秒:
秒: 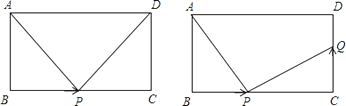
(1)![]()
![]() .(用
.(用 ![]() 的代数式表示)
的代数式表示)
(2) 当 ![]() 为何值时,
为何值时, ![]()
(3)当点 ![]() 从点
从点 ![]() 开始运动,同时,点
开始运动,同时,点 ![]() 从点
从点 ![]() 出发,以 v
出发,以 v![]() 的速度沿
的速度沿 ![]() 向点
向点 ![]() 运动,是否存在这样的v 值,使得
运动,是否存在这样的v 值,使得 ![]() 全等?若存在,请求出 v的值;若不存在,请说明理由.
全等?若存在,请求出 v的值;若不存在,请说明理由.
参考答案:
【答案】
(1)(10-2t)
(2)![]() 解:当t=2.5时,△ABP≌△DCP.理由如下:
解:当t=2.5时,△ABP≌△DCP.理由如下:
∵t=2.5,
∴BP=2t=2×2.5=5,
∴PC=10-5-5,
在△ABP和△DCP中,
∵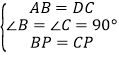 ,
,
∴△ABP≌△DCP(SAS).
(3)![]() 解:①当BP=CQ,AB=CP时,△ABP≌△PCQ.
解:①当BP=CQ,AB=CP时,△ABP≌△PCQ.
∵AB=6, BC= 10cm ,
∴PC=6,
∴BP=10-6=4,
依题可得:2t=4,
∴t=2,
∴CQ=BP=4,
∴2v=4,
∴v=2.
②当BA=CQ,PB=PC时,△ABP≌△QCP.
∵PB=PC, BC= 10cm ,
∴PB=PC=![]() BC=5,
BC=5,
依题可得:2t=5,
∴t=2.5,
∴CQ=BA=6,
∴2.5v=6,
∴v=2.4.
综上所述:当v等于2或2.4时△ABP与△PCQ全等.
【解析】解:(1)依题可得:BP=2t,
又∵BC= 10cm,
∴CP=10-2t,
所以答案是:10-2t.
【考点精析】本题主要考查了矩形的性质的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】m2(a﹣2)+m(2﹣a)分解因式的结果是( )
A. (a﹣2)(m2﹣m) B. m(a﹣2)(m+1)
C. m(a﹣2)(m﹣1) D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 , ∠AFB=∠ .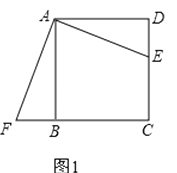
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ.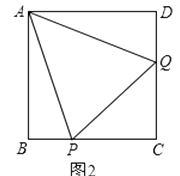
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:
课本研究三角形中位线性质的方法
已知:如图①,已知△ABC中,D,E分别是AB,AC两边中点.求证:DE∥BC,DE=
 BC.
BC.证明:延长DE至点F,使EF=DE,连接FC.…则△ADE≌△CFE.∴…


请你利用小亮的发现解决下列问题:
(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.

请你帮助小亮写出辅助线作法并完成论证过程:
(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x﹣y=5,xy=6,则xy2﹣x2y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式因式分解:
(1)m(m﹣5)﹣2(5﹣m)2;
(2)﹣4x3+8x2﹣4x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名同学本学期参加了相同的5次数学考试,老师想判断这两位同学的数学成绩谁更稳定,老师需比较这两人5次数学成绩的( )
A. 平均数 B. 中位数 C. 众数 D. 方差
相关试题

